격자 도형의 넓이 구하는 픽의 정리(Pick's theorem)
아마 대부분의 사람들이 픽의 정리를 들어본 적이 없을 것이다. 우리나라 교과과정에도 없고 KMO에서도 전혀 나오지 않는 내용이기 때문이다. 최근에 학원에서 이 정리에 대해 짧게 배운 적이 있다. 학원에서 들었을 때 꽤 흥미롭고 재미있어 보여서 추가로 찾아보았다. 여기서는 그런 내용들을 정리할 것이다. 또 이와 관련된 문제를 만들었는데, 그것도 풀어볼 것이다.
픽의 정리
꼭짓점이 격자점인 다각형에서 다각형의 내부에 있는 격자점의 수를 I 라고 하고, 다각형의 선분 위에 있는 격자점의 개수를 B라 할 때, 다각형의 넓이는
S = I + B/2 -1
로 나타낼 수 있다.
이것이 무슨 의미인지 직관적으로 이해가 가진 않지만 격자점에서 여러 도형의 넓이를 구해보면 픽의 정리가 성립함을 알 수 있다. 그럼 이제 증명을 해보자. 증명을 하기 전에, 모든 격자도형은 기본 격자 삼각형으로 분할할 수 있음과 기본 격자 삼각형의 넓이는 항상 1/2이라는 것을 알고 있어야한다.
기본 격자 삼각형 : 내부 격자점의 개수(I)가 0개이고, 선분 위에 있는 꼭짓점의 개수(B)가 3개인 격자 삼각형
p.f)
어떤 격자다각형에서, 이 도형을 모두 기본 격자 삼각형으로 쪼개었을 때의 기본 격자 삼각형의 개수를 k개라고 정의하자. 그러면 이 격자다각형의 넓이 S = 1/2 x k 로 표현된다. 또 k는 자명하게 이 격자다각형 내부의 격자점에서의 각들의 합을 180º로 나눈 것과 같다.
이제 격자다각형 내부의 모든 격자점들에 대한 각들을 더한 값을 구해보자.
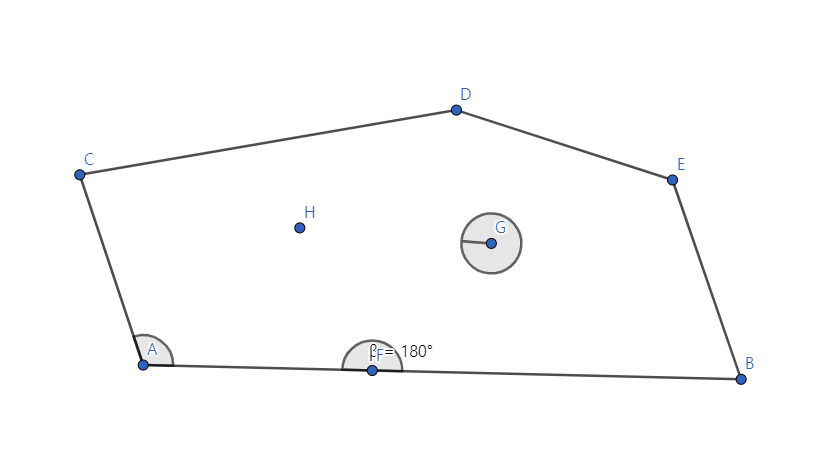
위와 같은 볼록한 도형에서 보면, 이 격자도형의 선분 위에 존재하는 격자점과 이 격자도형 내부에 존재하는 점으로 나눌 수 있다.
(1) 선분 위에 존재하는 격자점
1) 다각형의 꼭짓점인 격자점
구하는 것은 다각형의 내각의 합과 같으므로, 180º (B1-2)가 된다. (단, B1은 꼭짓점 개수)
2) 다각형의 꼭짓점이 아닌 격자점
이 경우 항상 각이 180º 가 되므로, 180º B2 가 된다. (단, B2는 꼭짓점이 아닌 선분 위 격자점 개수)
(2) 도형 내부 격자점
도형 내부 격자점 개수는 I 개이고, 항상 360º이므로, 360º I
∴ 도형의 전체 각의 크기는 180º (B1-2) + 180º B2 + 360º I = 180º (B - 2) + 360º I
→ k = 2I + B -2
→ S = k/2 = I + B/2 -1
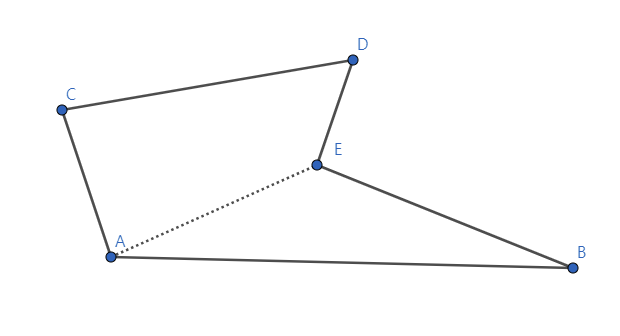
위와 같은 오목한 격자다각형의 경우, 볼록한 격자다각형으로 분할하는 것이 가능하다. 따라서 픽의 정리를 만족하는 도형을 붙혀 만든 도형도 픽의 정리를 만족함을 보이기만 해도 충분하다. 증명은 수학적 귀납법으로 하면 되는데, 나중 도형의 넓이를 처음 도형들의 넓이의 합으로 표현해서 정리해주면 쉽게 보일 수 있으므로 생략하겠다.
이제 이와 관련된 문제를 풀어보자.
볼록한 격자오각형의 최소넓이는 얼마인가?
Sol) 먼저 볼록 격자오각형의 각 꼭짓점의 좌표를 (a1,b1),(a2,b2) .... (a5,b5)와 같이 표현해보자.
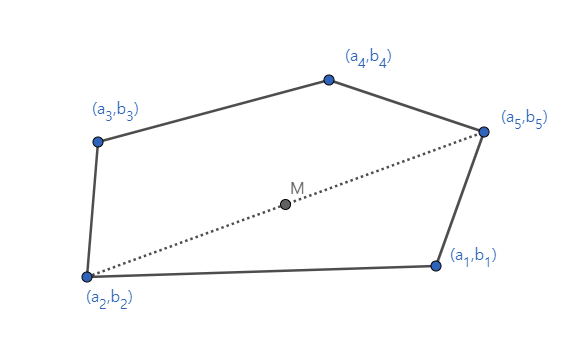
Claim) 볼록 격자오각형은 내부의 격자점을 반드시 한 개 이상 포함한다.
p.f) 어떤 두 좌표 (ai,bi),(aj,bj)에 대해 a끼리 기우성이 같고, b끼리 기우성이 같으면, 이들의 중점도 격자점이 된다. 따라서 가능한 기우성 조합을 생각해보면 총 4개인데 꼭짓점이 5개이므로, 비둘기집의 원리에 의해서 기우성이 같은 쌍이 존재한다. 따라서 적어도 한 쌍의 꼭짓점의 중점은 격자점 위에 존재한다.
∴ 내부 격자점 개수 I ≥ 1이다. 선분 위 격자점 개수 B ≥ 5이므로 넓이 S ≥ 1 + 5/2 - 1 = 5/2.
S = 5/2인 경우, 자명한 실례가 존재하므로 최소인 경우 넓이는 5/2이다.