정삼각형 격자에서 정삼각형 개수 세기

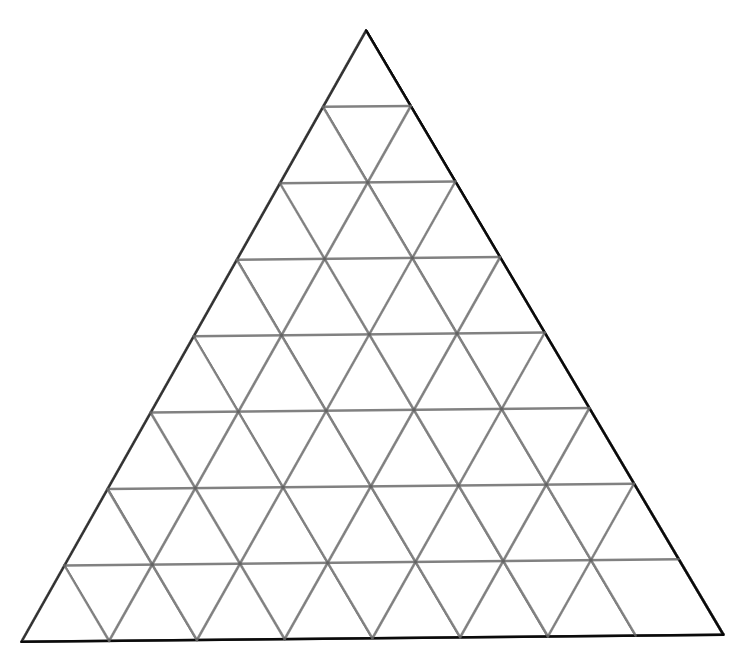
 n²개의 정삼각형으로 이루어진 정삼각형 격자에서 정삼각형의 개수는 어떻게 셀까? 이 포스팅에서는 이에 대한 일반화를 해보려고 한다.

 

 먼저 이러한 문제는 점화식으로 접근하는 것이 쉬울 것 같다. 먼저 사용할 점화식을 정의해주자.

a(n,k) = |한 변의 길이가 n인 정삼각형 격자에서 한 변의 길이가 k인 정삼각형의 개수|

 자명하게 a(n,1) = n², a(n,n) = 1이다. 이제 a(n,k)에 대해서 생각해보자.

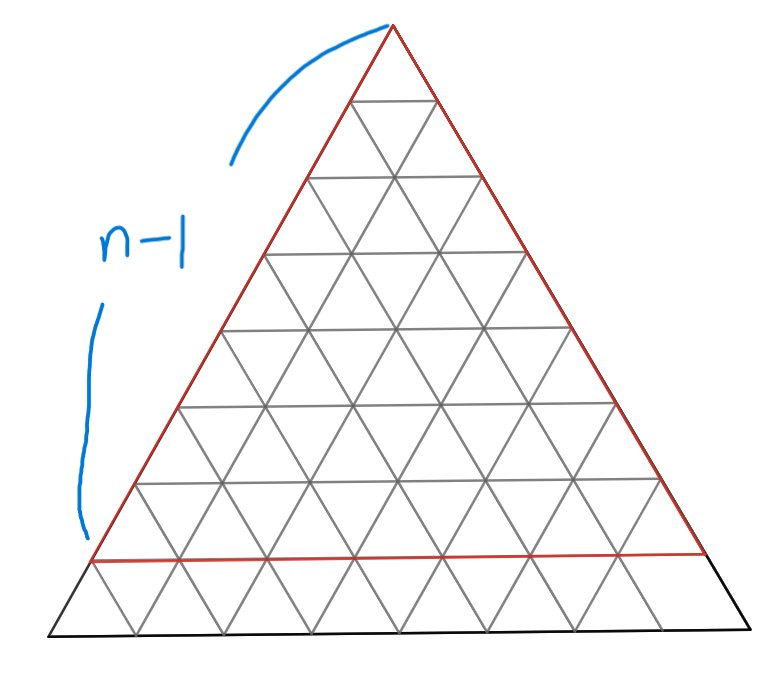
 a(n,k) 을 계산할 때 위 그림에서도 볼 수 있듯이 a(n-1,k)에 새로 추가되는 정삼각형들을 더해주면 된다. 그럼 새로 추가되는 정삼각형의 개수를 구해보자.

 

1) 큰 정삼각형과 변이 평행한 정삼각형

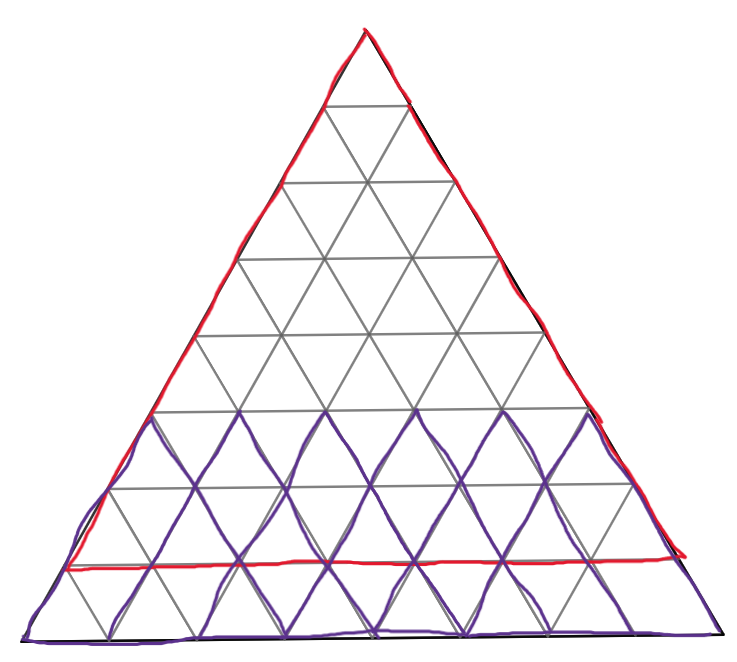
이 경우는 구하는 정삼각형은 보라색 정삼각형이므로, n-k+1개가 된다.

 

2) 큰 정삼각형과 변이 평행하지 않은 정삼각형

      1> n≤2k-2

         이 경우에는 역삼각형이 추가되지 않는다.

      2> n>2k-2

         이 경우에는 n-k-1개씩 역삼각형이 추가된다.(n=2k-1인 경우는 0개 추가됨)

 

∴a(n,k) = a(n-1,k) + n - k + 1                          (n≤2k-2)
             = a(n-1,k) + (n - k + 1) + (n - k - 1)     (n>2k-2)
             = n²                                                              (k=1)
             = 1                                                                (n=k)

 

 이제 이 점화식을 계산해보자.

1) n≤2k-2
 a(n,k)  = a(n-1,k) + n - k + 1
            = a(n-2,k) + (n - k + 1) + (n-1 - k + 1)
            = .....
            = a(k,k) + ∑(i - k + 1)         (k+1 ≤ i ≤n)
            = 1 + (n-k)(n+k+1)/2 - (k-1)(n-k)
            = (k² + n² - 3k + 3n - 2nk + 2)/2
            = ((n - k + 3/2)² - 1/4)/2

2) n>2k-2
 a(n,k) = a(n-1,k) + 2n - 2k
           = a(n-2,k) + (2n - 2k) + (2n-2 - 2k)
           = .....
           = a(2k-2,k) + ∑(2i -2k)      (2k-1 ≤ i ≤ n)
           = ((k-1/2)² - 1/4)/2 + n² + n - 2kn + 2k -2
           = (k² + 2n² + 3k + 2n - 4kn - 4)/2 

 점화식 계산이 조금 힘들지만 이렇게 구할 수 있다. ㅎㅎ

 

+추가로 dp를 이용해서 n에 대해서 모두 구하는 코드도 짜보았다.

#include <iostream>
using namespace std;

int a[100][100];

int main()
{
    int A,k,n;
    cin>>A;
 
    for(k=1;k<=A;k++)
    {  
        if(k==1)
        {
            a[A][k] = A*A;
        }
        else{
                for(n=k;n<=A;n++)
                {
                    if(n == k)
                    {
                        a[n][k] = 1;
                    }
                    else
                    {
                        if(n<=2*k-2)
                        {
                            a[n][k] = a[n-1][k] + n-k+1;
                        }
                        else
                        {
                            a[n][k] = a[n-1][k] + 2*n - 2*k;
                        }
                    }
                }
            }
       
        cout<<k<<" : "<<a[A][k]<<"\n";
    }
}