페르마 포인트, 스타이너 포인트와 그의 확장
아마 KMO를 공부했던 사람이라면 페르마 포인트(Fermat Point)나 스타이너 포인트(Steiner Point)에 대해 들어본 적이 있을 것이다. 이들 모두 주어진 임의의 점들에 대한 기하 중앙값(Geometric median)과 관련이 있다. 이 글에서는 이들의 증명과 가중치가 주어질 경우에 대해서는 어떻게 하는지에 대한 내용을 정리하려고 한다. 아직 일반적인 증명을 할 정도까지의 수준은 아니기 때문에 삼각형과 사각형에 대해서 다룰 것이다.
기하 중앙값(Geometric median)의 정의 : 유클리드 평면에서 주어진 샘플 점들에 대해, 각각의 점들까지의 거리의 합이 최소가 되도록 하는 점
출처 : https://en.wikipedia.org/wiki/Geometric_median
Geometric median - Wikipedia
From Wikipedia, the free encyclopedia Point minimizing sum of distances to given points Example of geometric median (in yellow) of a series of points. In blue the Center of mass. In geometry, the geometric median of a discrete set of sample points in a Euc
en.wikipedia.org
1. 페르마 포인트(Fermat Point)
1) 모든 내각의 크기가 120° 미만인 경우
작도)

잘 알려져 있다시피, 각 변에서 삼각형 외부로 정삼각형을 잡고, 나머지 꼭짓점과 연결해 만든 변들의 교점이 바로 페르마 포인트가 된다. 그림에서 변 BD와 삼각형 ADC의 외접원의 교점으로 잡아도 된다.
증명)
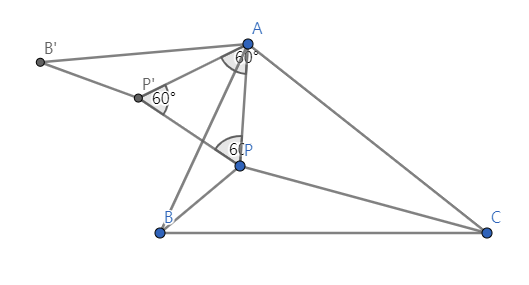
삼각형 내부의 임의의 점 P를 잡자. A를 기준으로 △ABP 를 60 °회전 시켜 삼각형 △AB ′ P ′ 을 만들자. △ABP 와 삼각형 △AB ′ P ′ 은 서로 합동이므로 선분AP = 선분AP' 이고, 선분BP = 선분BP'이다.
따라서 선분AP + 선분BP + 선분CP = 선분 PP' + 선분 B'P' + 선분 PC ≤ 선분 B'C' 가 성립한다. 등호가 성립할 경우는 B',P',P,C가 공선점일 경우이므로, 점 P가 페르마 포인트이기 위해선 선분 B'C 위에 존재해야한다. 마찬가지 방법으로 선분 AC에서도 하면, 점 P가 유일하게 결정된다.
2) 크기가 120° 이상인 내각이 존재하는 경우

이런 식으로 한 내각의 크기가 120°를 넘어가는 경우에는 교점이 삼각형 내부에 생기지 않게 된다. 일반성을 잃지 않고 B의 각도가 120°이상이라고 하자. 이때 선분 PP' + 선분 B'P' + 선분 PC값은 P의 위치의 관계없이 선분 BB' + 선분BC보다 작거나 같으므로 P가 B일 때가 최소이다.
2. 스타이너 포인트(Steiner Point)
스타이너 포인트는 페르마 포인트를 조금 확장한 것으로, 여러 다각형에서 각 꼭짓점까지의 거리의 합이 최소인 점이며, 페르마 포인트와 달리 개수가 1개일 필요가 없다. 참고로 볼록 n각형(n≥3)에서 스타이너 포인트의 개수는 항상 n-2개 이하이다(각 정점들의 차수와 간선 개수의 관계로 쉽게 증명할 수 있다.) . 또한 스타이너 포인트를 이용해 그래프의 길이를 가장 짧게 만들었을 때의 그래프를 스타이너 트리라고 한다. 스타이너 트리에서 각 변 사이의 각도는 120º이상이며(증명은 귀류법으로 쉽게 가능), 이러한 특성에 의해 각 점의 차수는 3(1이나 2의 경우는 모순임을 보일 수 있음)이다.

증명) 볼록사각형인 경우
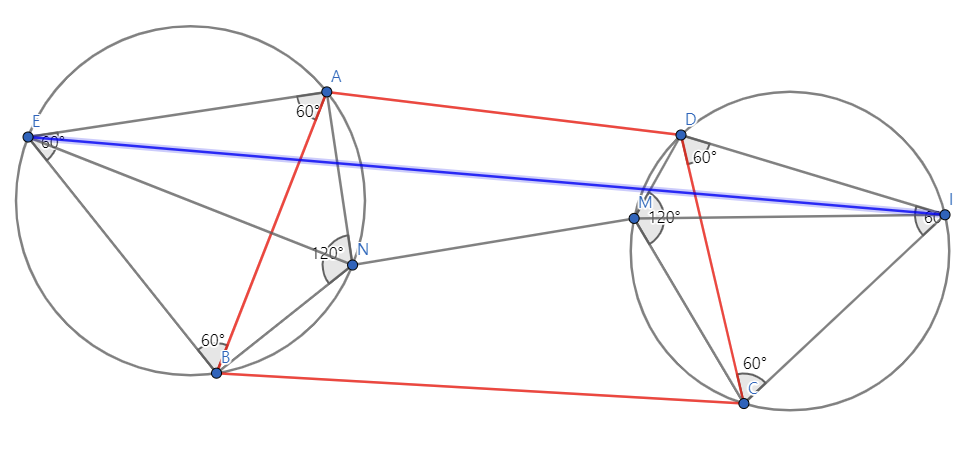
앞서 말한 스타이너 트리의 성질에 의해 N과 M이 스타이너 포인트라면 각각 △ABE, △CDI의 외접원 위에 존재할 것이다. 이때 선분 AN + 선분 NB는 자명하게 선분 EN과 같고, 선분 DM + 선분 MC는 선분 MI와 같으므로, 구하는 길이 선분 AN + 선분 BN + 선분 NM + 선분 MD + 선분 MC = 선분 EN + 선분 NM + 선분 MI이다. 또 이 길이는 위치에 상관없이 선분 EI보다 작거나 같으므로 최소인 경우는 E, N, M, I가 공선점인 경우이다.
일반적으로 위치를 찾는 방법은 잘 모르겠지만 볼록오각형, 볼록육각형에 대해서는 직접 해보았다. 나중에 더 일반적인 방법을 찾으면 추가로 적어볼 계획이다.
3. 확장(가중치가 주어진 경우)
가중치가 주어진 경우에 대해서는 페르마 포인트를 처음 배웠을 때 증명 방식을 조금 응용해서 시도해보았다. 삼각형의 경우, 페르마 포인트 증명 과정 중에서 삼각형을 회전시킬 때 나선닮음을 이용해서 풀어주면 쉽게 해결이 된다.
평면 위에 예각삼각형 ABC가 있다. 평면 위의 점 X에 대해 pAX + qBX + rCX가 최소가 되도록 하는 점 X의 위치를 찾아라.
1) p,q,r을 길이로 하는 삼각형을 만들 수 없는 경우
이 경우는 단순하게 p,q,r 중 하나의 값이 다른 것들에 비해 클 경우로 생각해 볼 수 있다. 일반성을 잃지 않고 p > q + r이라고 하면 직관적으로 생각해봐도 X가 A여야한다는 것을 알 수 있다.
2) p,q,r을 길이로 하는 삼각형을 만들 수 있는 경우
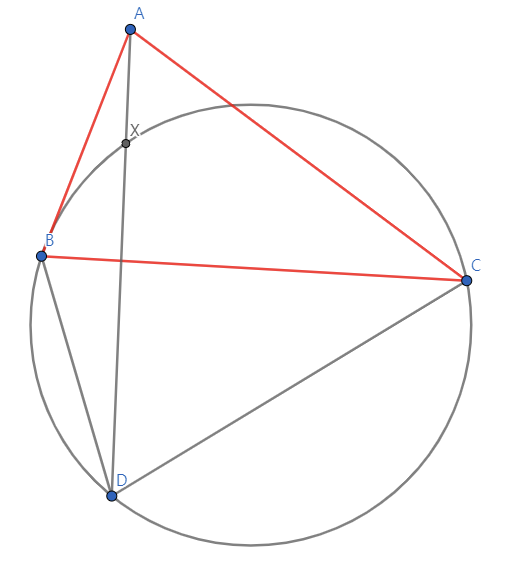
X를 작도하는 것은 선분 BC : 선분 CD : 선분 BD = p : q : r 이 되도록 △ABC 외부에 △BCD를 잡은 다음, 선분 AD와 △BCD의 외접원의 교점을 작도해주면 된다.
증명)
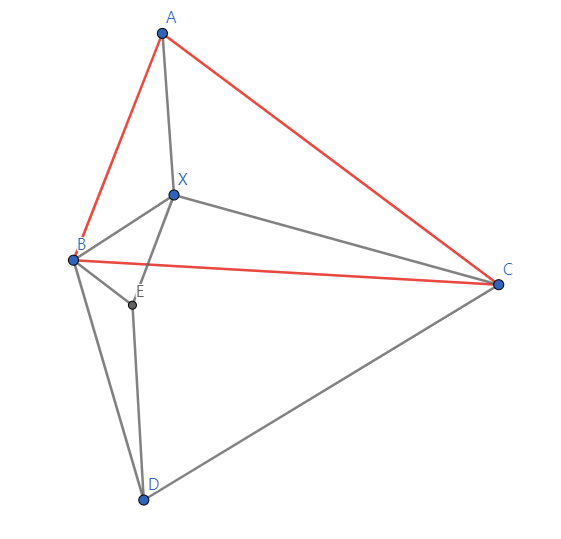
먼저 아까와 똑같이 △BCD를 잡아주고, 선분 BC가 선분 BD가 되도록 △BCX를 회전시켜 △ BDE를 만든다. 그러면 △BDE와의 닮음비가 선분 BC : 선분 BD = p : r 이 된다. 따라서 선분 ED = r/p CX이고, 나선닮음으로 인한 파생 닮음인 △BDC와 △BXE에서 선분 BX : EX = p : q이므로 선분 EX = q/p BX이다. 결론적으로 pAX + qBX + rCX = p(AX + q/p BX + r/p CX) = p (AX + XE + ED) ≤ p AD이다. 등호가 성립할 때에는 A,X,E,D가 공선점이며, 이때는 ∠XDB = ∠XCB가 되므로 X,B,D,C는 공원점이다.