몬즈의 정리(Monge's Theorem)

  몬즈의 정리(Monge's Theorem)는 KMO 2차에 자주 나오는 정리로 근축에 대해 배울 때 꼭 배워야히는 정리 중 하나이다. 여기서는 몬즈의 정리와 이와 관련된 재미있는 문제 몇 개를 풀어볼 것이다.

몬즈의 정리 : 세 원 A,B,C가 두 점에서 서로 교차할 때, 세 공통현은 한 점에서 만난다. ( 세 원의 근축들은 공점선이다.)

 

참고하면 좋은  사이트 : https://en.wikipedia.org/wiki/Power_center_(geometry)

Power center (geometry) - Wikipedia

 

 

 1. 몬즈의 정리(Monge's Theorem) 증명

 

 몬즈의 정리의 증명은 근축을 잘 이해하고 있다면 아주 쉽게 증명할 수 있다. 

 

증명)

 

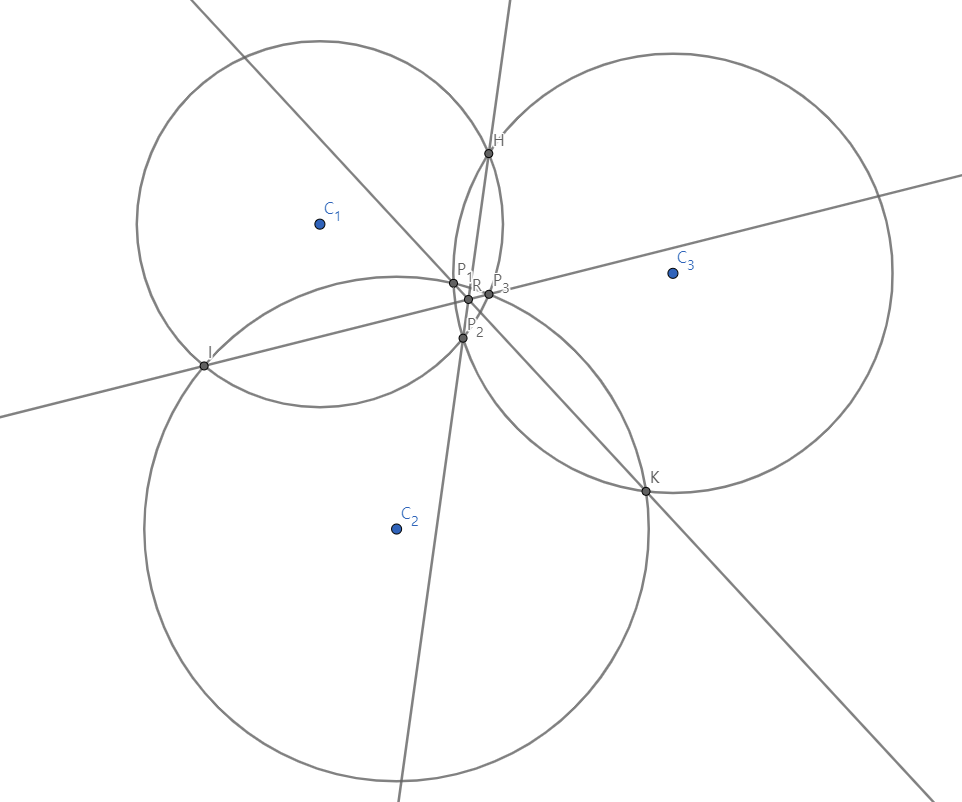
 세 원 C1, C2, C3가 있고, C1, C2의 두 교점, C2, C3의 두 교점, C3, C1의 두 교점을 각각 P3, I, P1, K, P2, H라고 하자. 직선 P3I와 직선 P2H의 교점을 R이라고 하자. 직선 P3I는 C1, C2의 근축이고, 직선 P2H는 C1, C3의 근축이므로 점 R에서는 C1, C2, C3와의 방멱값이 모두 같다. 따라서 R은 근심이고, C2와 C3의 근축인 직선 P1K 위에도 존재한다. 

 

 세 원이 교차하고 있지 않더라도 세 원의 근축이 공점선이라는 것은 똑같이 증명할 수 있다.

 

 

2. 문제

 예각 삼각형ABC와 외접원 w가 있다. ∠A의 이등분선이 w와 만나는 점을 M, BC에 평행한 직선이 AC, AB와 만나는 점을 각각 X, Y라 하고 MX, MY가 w와 만나는 점을 각각 S,T라 하고, XY와 ST의 교점을 P라 할 때, PA가 w의 접선임을 증명해라.

  

Solution)

 

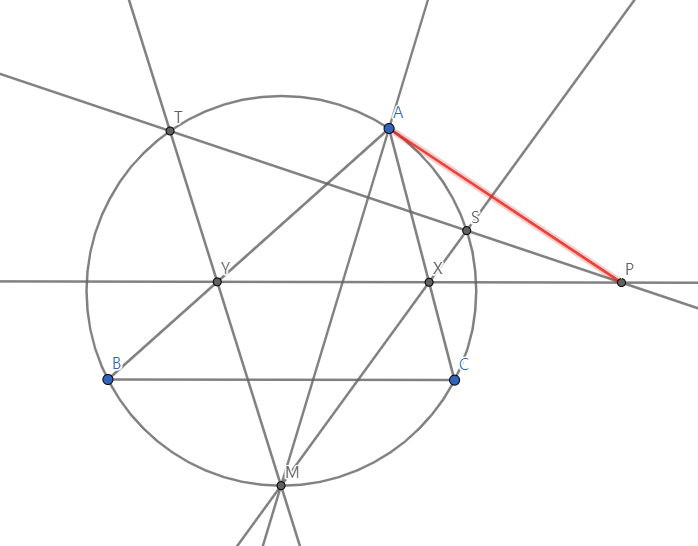
 먼저, S,X,Y,T가 공원점이라고 생각해보자. □SXYT의 외접원, △AXY의 외접원, △ABC의 외접원(원 w)을 보면, 직선 TS와 직선 YX,  접점이 A인 원 w의 접선이 모두 근축이라는 사실을 알 수 있다. 따라서 PA가 접선일 필요충분조건은 몬즈의 정리에 의해 S,X,Y,T가 공원점인 것이다. 

 

W.T.S  S,X,Y,T 공원점 ⇔ ∠TYX = ∠PSM (내대각)

                                                   = ∠TBM ( □ TBMS에서 내대각)

∠TYX = ∠TYA + ∠AYX

          = ∠BTY + ∠TBY + ∠ABC

          = ∠MCB + ∠TBY + ∠ABC

          = ∠TBM

 

 

 두 개의 반지름이 다른 원 C1, C2는 서로 다른 두 점 M, N에서 만난다. C1, C2는 가각 중심이 O1, O2이고 중심이 O인 원에 모두 내접한다. 접점을 각각 S,T라 하자. OM ⊥ MN임과 S,N,T 세 점이 일직선에 놓임은 필요충분조건임을 증명하여라.

 

Solution)

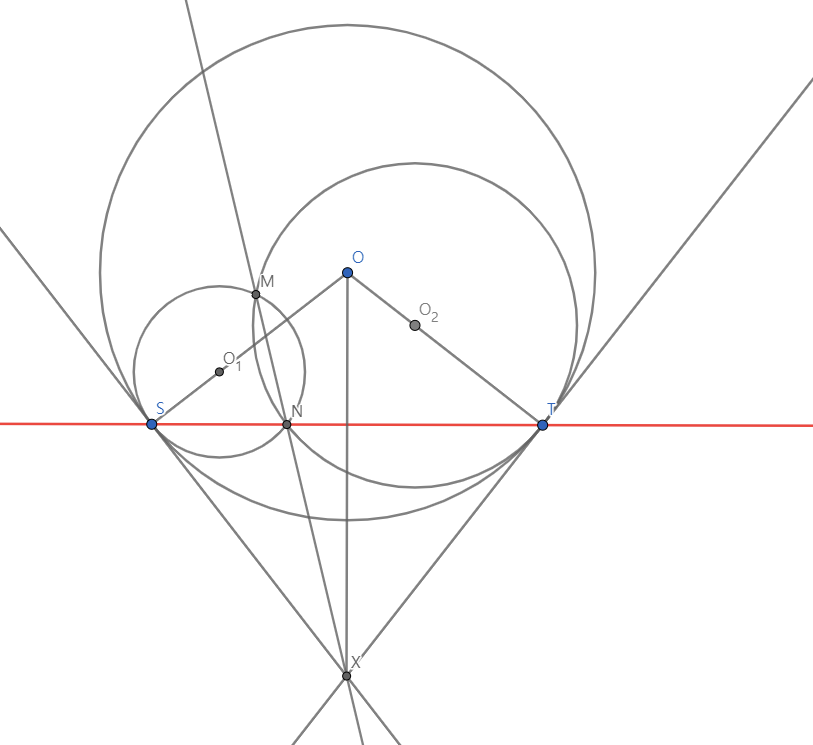
점 X를 세 원 C1,C2,O의 근축들의 교점이라고 하자.

점 Y를 선분 OX와 선분 ST의 교점이라고 하자.

 

1) S,N,T 공선점 ⇒ OM ⊥ MN 증명

∠OSX = ∠OTX = 90º

∠OYS = 90 º

∠SOX = ∠ ● 라고 하자.

∠ STX =  ∠SOX = ∠ ● (O,S,X,T가 공원점)

⇒ ∠OST = 90 º - ∠ ●

⇒ ∠SO1N = 2 ∠ ● (△SO1N이 이등변삼각형)

⇒ ∠ SMN = ∠  ●

 

∴ ∠ SMN = ∠SOX = ∠ ● 이므로 S,M,T,X 공원점

⇒ O,S,X,T도 공원점이므로 S,M,T,X,O 공원점

⇒ ∠OMN = ∠OMX = 180 º - ∠OTX = 90 º

 

2) OM ⊥ MN ⇒ S,N,T 공선점 증명

∠ OMN = 90º

⇒ O,M,S,X,T 공원점

선분 ST와 직선 MN의 교점을 N'이라하자.

W.T.S  N = N'

∠ SN'X = ∠ SMN + ∠ MST

             = ∠ MXT + ∠ XTS ( ∠ MST  = ∠ XTS 인 이유는 1)에 나와 있음)

             = ∠ SNX                                                

 

 

 

 

 

 중심이 O이고, △ABC의 꼭짓점이 A와 C를 지나며 변 AB, BC와 각각 B가 아닌 점 K와 N에서 만나는 원이 있다.
△ABC의 외접원과 △KBN의 외접원이 정확히 두 점 B와 M에서 만나면, ∠OMB는 직각임을 증명하시오.

 

증명)

 

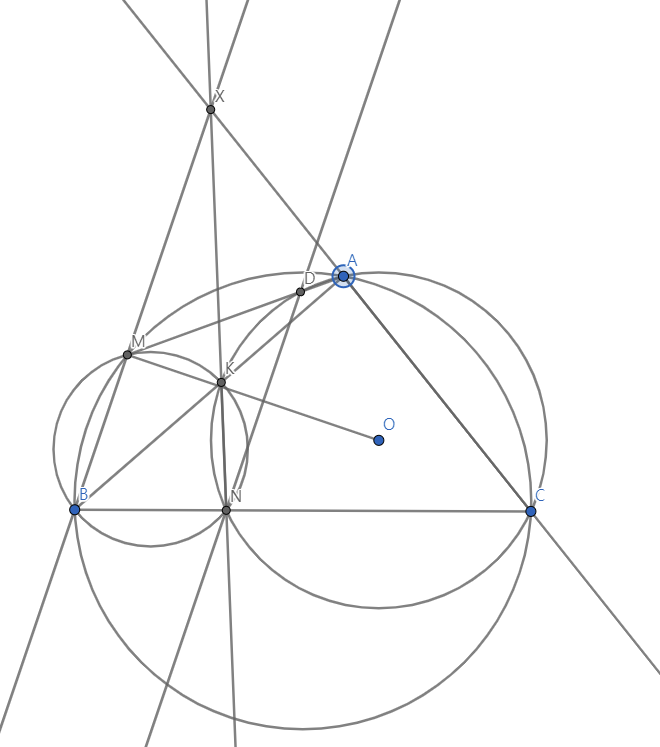
 세 원의 근축들의 교점을 X라 하자.

또, 선분 AM위에 선분ND // 선분 BM이 되도록 하는 점 D를 잡자.

∠MDN = ∠DMX

            = ∠ACB

⇒A,D,K,N,C 공원점

∠MDN = ∠C = ∠BKN

           = ∠BMN

           = ∠MND

⇒선분 MD = 선분 MN

선분 DO = 선분 NO이므로 사각형 MDON에서 선분 OK ⊥선분 DN

⇒선분 OM ⊥ 선분 MB