티스토리 뷰
문제 풀이
이 문제는 그래프가 주어질 때 서로 연결되어있는 정점이 없도록 최대한 많은 정점을 선택하는 문제이다. 처음 보자마자 이색 염색이 떠오르긴 했지만 홀수사이클이 존재하는 경우에는 이색 염색이 안되므로 다른 방법으로 해야한다.
Case 1) 쪽방이 아예 존재하지 않는 경우(∀$C_{i} = 0$)
N = 1 → 1마리
N = 2k or N = 2k+1→ k마리
Case 2) 쪽방이 존재하는 경우
먼저 당연하게 쪽방의 개수가 1개 이상인 칸에 경우 쪽방에만 개미를 배치하는 것이 유리하다. 그럼 쪽방에 있는 방을 기준으로 구간을 나누어볼 수가 있다.
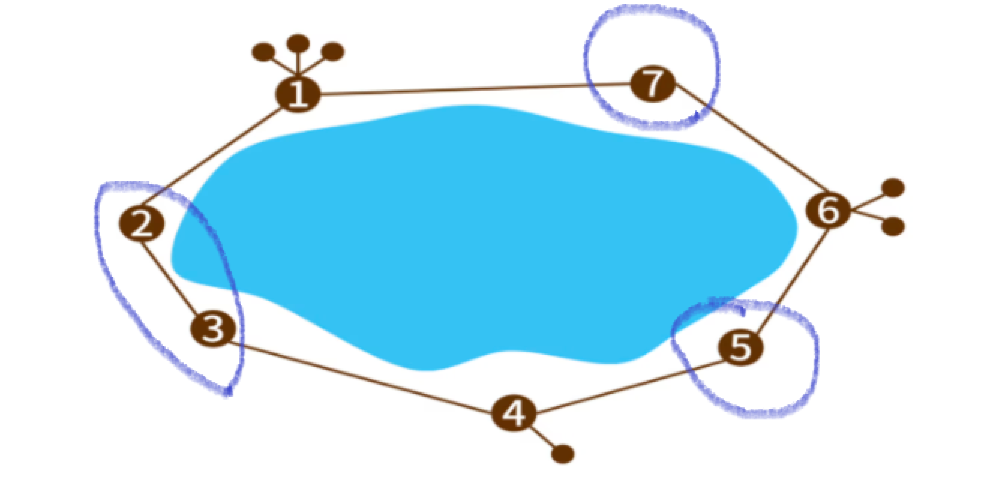
문제의 예시에서는 쪽방이 존재하는 방은 1, 4, 6으로 3개이다. 이 3개를 기준으로 구간이 3개로 나뉘게 된다. 이때 1,4,6에는 쪽방에만 개미가 들어가므로 1,4,6방에는 개미가 없다. 따라서 문제는 각 구간에서 배치 가능한 개미들의 개수로 바뀌게 된다. 여기서는 구간 [2,3],[5],[7]에서 모두 최대 1마리까지밖에 배치할 수 없으므로 답은 4 + 3 = 7 이 된다. 구간의 길이를 $l_{i}$이라고 하면 가능한 개미의 최대 개수는 아래와 같이 나타낼 수 있다.
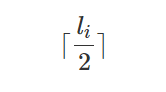
결론적으로 전체 최대 개미 개수는 아래와 같이 나타낼 수 있다.
$$\sum C_{i} + \sum\lceil\frac{l_{i}}{2}\rceil$$
시행 착오
1) 개수를 int 범위로 해놔서 오버플로우가 났다.
2) cin.tie(0); cout.tie(0); ios::sync_with_stdio(0); 안해놔서 시간초과가 났다.
3) Case1 에서 Case2랑 똑같이 올림함수로 해놔서 틀렸다.
코드
#include <iostream>
using namespace std;
long long N,C,n=0,k=999,l;
bool arr[250010];
int main()
{
cin.tie(0);
cout.tie(0);
ios::sync_with_stdio(0);
cin>>N;
for(int i=1;i<=N;i++)
{
cin>>C;
if(C==0)continue;
arr[i] = true;
k=i-N;
n+=C;
}
long long m = N+k;
if(k==999)
{
if(N==1) n = 1;
else n = N/2;
cout<<n; return 0;
}
for(long long i=1;i<=m;i++)
{
if(!arr[i]) continue;
l = i;
n += (l-k)/2;
k = l;
}
cout<<n;
}'Computer Science > BOJ' 카테고리의 다른 글
| BOJ 19942. 다이어트 (0) | 2024.07.13 |
|---|---|
| BOJ 14500. 테트로미노 (1) | 2024.06.08 |
| BOJ 28218. 격자 게임 Game Strategy (0) | 2024.05.11 |
| BOJ 1005. ACM Craft (0) | 2024.04.21 |
| BOJ 16891. 탄성충돌 (0) | 2024.03.24 |
