티스토리 뷰
반응형
SCC는 모든 정점에서부터 모든 정점까지로의 경로가 존재하는 그래프를 의미한다. 주어진 그래프에서 SCC들을 찾아내는 알고리즘은 타잔 알고리즘과 코사라주 알고리즘이 있다. 아직 정확히는 모르지만 타잔 알고리즘이 더 활용도가 높다고 하므로 타잔 알고리즘을 공부했다.
1) 타잔 알고리즘의 동작
기본 원리는 dfs와 같다.
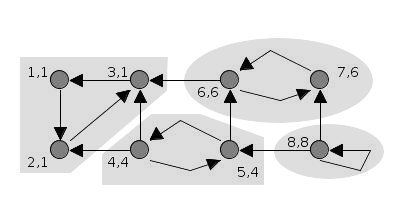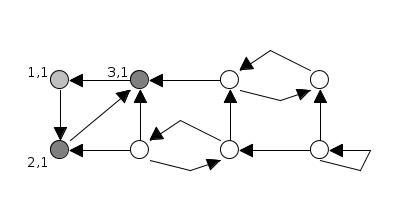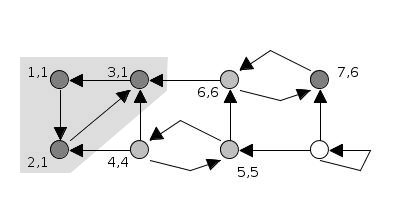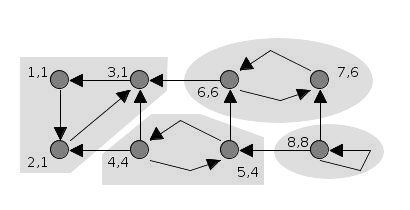
어떤 정점에서 시작해 dfs를 하는데 방문하는 정점마다 서로 다른 idx를 부여한다. dfs 결과 자기 자신의 idx가 나온다면 cycle(SCC)가 존재한다는 것을 알 수 있다.
2) 타잔 알고리즘의 구현
구현은 dfs와 stack을 이용하여 한다.
1> dfs
int v, e, id;
int d[MAX];
int sccNum;
int sn[MAX];
vector<int> a[MAX];
bool finished[MAX];
stack<int> s;
vector<vector<int>> SCC;
int DFS(int c) {
d[c] = ++id;
s.push(c);
int result = d[c];
for (int next : a[c]) {
if (d[next] == 0) result = min(result, DFS(next));
else if (!finished[next]) result = min(result, d[next]);
}
if (result == d[c]) {
vector<int> scc;
while (true){
int t = s.top();
s.pop();
scc.push_back(t);
finished[t] = true;
sn[t] = sccNum;
if (t == c) break;
}
sort(scc.begin(), scc.end());
SCC.push_back(scc);
sccNum++;
}
return result;
}idx는 0부터 시작해서 각 정점마다 다른 값으로 부여된다. 각 정점을 탐색하면서 stack에 넣어주고 그 정점에서 갈 수 있는 정점으로 이동하면서 부모값(result)를 구한다. 만약 구한 부모값이 자신의 idx와 같다면 stack에 있는 정점들을 차례대로 pop과 방문처리를 해주다가 자신이 stack에서 나오면 종료한다.
2> scc
void scc(){
for (int i = 1; i <= v; i++) {
if (d[i] == 0) DFS(i);
}
cout<<sccNum<<"\n";
sort(SCC.begin(),SCC.end(),compare);
for (auto& currSCC : SCC) {
for (int curr : currSCC){
cout<<curr<<" ";
}
cout<<-1<<"\n";
}
}$d[i] = 0$(한번도 탐색되지 않은) 정점들에 대해서 DFS를 해준다.
'Computer Science > Algorithm' 카테고리의 다른 글
| BitMasking DP를 이용한 TSP (1) | 2024.12.11 |
|---|---|
| Segment Tree (5) | 2024.08.17 |
| Topology Sort (0) | 2024.07.15 |
| Floyd-Warshall Algorithm (0) | 2024.07.15 |
| Dijkstra Algorithm (0) | 2024.07.15 |
