티스토리 뷰
반응형
문제 풀이
이 문제는 Hilbert Curve 모양의 미로에서 시작점까지의 거리가 주어질 때 그 위치의 좌표를 구하는 문제이다.
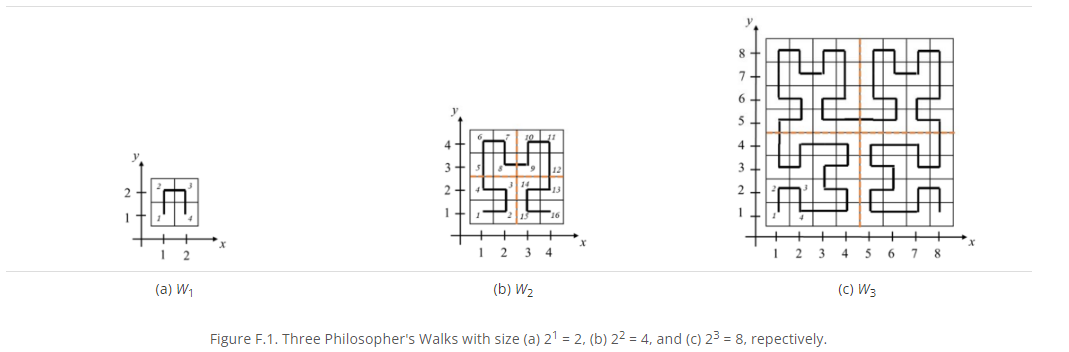
입력은 $n \leq 2^{15}$ 와 $m \leq n^2$ 이 주어지는데 $n$은 미로의 크기, $m$은 구하고자 하는 점의 시작점으로부터의 거리이다.
Hilbert Curve가 재귀적으로 정의되는 모양이다보니까 이 문제도 재귀적으로 풀어야겠다는 생각을 했다. 이 때 미로를 $\frac{n}{2}$ 크기의 네 구역으로 나누어서 분할정복 알고리즘으로 플 수 있다고 생각했다. 그래서 먼저 좌표를 반환해주는 함수를 다음과 같이 정의해보자.
//pair<x좌표,y좌표> : 크기 k인 미로에서 거리 d인 점의 좌표
pair<int,int> calcCoord(int k, int d)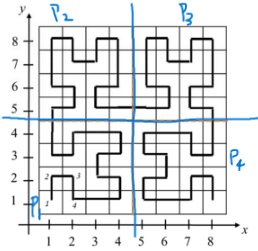
먼저 구하고자 하는 점이 P1에 있다고 하면 $calcCoord(\frac{k}{2},d)$을 y = x 기준으로 반전시킨 것과 같으므로 다음과 같이 표현된다.
pair<int,int> c1 = calcCoord(k/2,d);
if(phase == 1){
return {c1.second, c1.first};
}
P2와 P3는 크기가 $\frac{k}{2}$인 미로에서 아무런 회전도 하지 않았으므로 더 쉽게 표현할 수 있다.
pair<int,int> c2 = calcCoord(k/2,d-(k/2)*(k/2));
pait<int,int> c3 = calcCoord(k/2,d-2*(k/2)*(k/2));
if(phase == 2){
return {c2.first, c2.second + k/2};
} else if(phase == 3){
return {c3.first + k/2, c3.second + k/2};
}
P4는 이전 미로를 반시계 방향으로 90도 회전한 상태이다. 그래서 P4의 가장 오른쪽 위 점을 기준으로 이전 계산 값을 빼주면 되는데 조심해야할 것을 x좌표와 y좌표를 바꿔서 빼줘야한다.
pair<int,int> c4 = calcCoord(k/2,d-3*(k/2)*(k/2));
if(phase == 4){
return {k - c4.second + 1, k/2 - c4.first + 1};
}
코드
#include <iostream>
#include <algorithm>
using namespace std;
int n,m;
void input(){
cin>>n>>m;
}
pair<int,int> calcCoord(int k, int d){
if(k == 2){
if(d == 1) return {1,1};
else if(d == 2) return {1,2};
else if(d == 3) return {2,2};
else return {2,1};
}
int phase = 1;
int phaseLength = (k/2)*(k/2);
while(d>phaseLength){
d -= phaseLength;
phase ++;
}
pair<int,int> c_prime = calcCoord(k/2,d);
if(phase == 1){
return {c_prime.second, c_prime.first};
} else if(phase == 2){
return {c_prime.first, c_prime.second + k/2};
} else if(phase == 3){
return {c_prime.first + k/2, c_prime.second + k/2};
} else if(phase == 4){
return {k - c_prime.second+1, k/2 - c_prime.first + 1};
}
}
void solve(){
pair<int,int> c = calcCoord(n,m);
cout<<c.first<<" "<<c.second;
}
int main(){
cin.tie(0);
cout.tie(0);
ios::sync_with_stdio(0);
input();
solve();
}'Computer Science > BOJ' 카테고리의 다른 글
| BOJ 32074. XOR 최대 (1) | 2024.10.26 |
|---|---|
| BOJ 1422. 숫자의 신 (2) | 2024.10.08 |
| BOJ 1019. 책 페이지 (2) | 2024.08.31 |
| BOJ 15486. 퇴사 2 (2) | 2024.08.27 |
| BOJ 2887. 행성터널 (2) | 2024.08.17 |
