물체를 경사로 떨어뜨리는데 걸리는 최소 시간

 

 

 높이가 $h$인 지점에 있는 질량 $m$의 물체를 벽에서부터 막대를 이용해 경사각이 $θ$인 경사까지 굴릴 때 걸리는 최소 시간은? 그리고 그때의 막대의 길이는? 

 

 문제만 놓고 보면 굉장히 쉬운 문제 같아보이지만 처음 접근할 땐 생각을 많이 해봐야한다. 이 문제를 풀어보기 전에 조금 더 쉬운 문제를 한 번 보자.

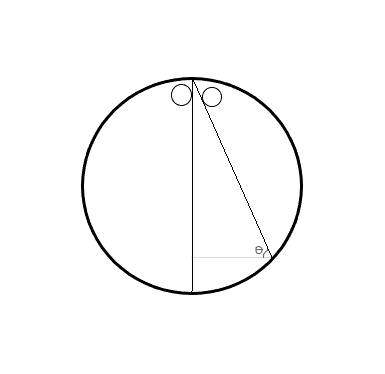
 어떤 원에서 지표와 수직한 지름으로 공을 떨어뜨릴 때 걸리는 시간과 다른 호로 공을 떨어뜨릴 때 걸리는 시간이 같을까? 이건 자명하게 같다. 왜냐하면 둘 다 등가속도 운동을 하는데, 가속도의 비는 1 : sinθ이고, 거리비는 sinθ : 1이기 때문에 쉽게 알 수 있다. 

 

 그럼 이것을 이용해 이 문제를 풀어보자.

P:물체의 위치

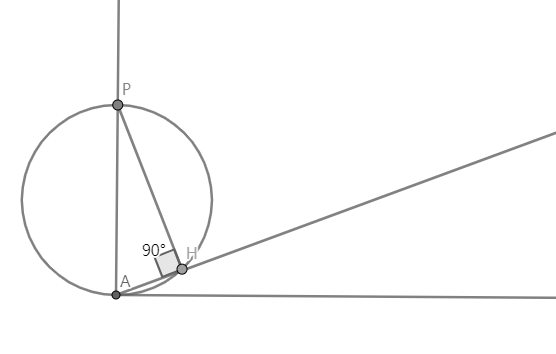
$\overline{PA}$를 지름으로 하는 원을 그리고, 그 원과 경사의 교점을 $H$라고 해보자. $∠PHA$는 지름에 대한 원주각이므로 $90˚$일 것이다.  그리고 위에서 밝힌 사실에 의해서 공을 막대 $\overline{PH}$로 떨어뜨리는데 걸리는 시간은 $P$에서 $A$로 자유낙하하는데 걸리는 시간과 같다. 이렇게 그리고 보면, 막대는 선분 $\overline{AH}$위에 있는 어떤 점에 놓여야한다는 것을 쉽게 알 수 있다. 이제 이 원을 조금 더 축소해서 그려보자.

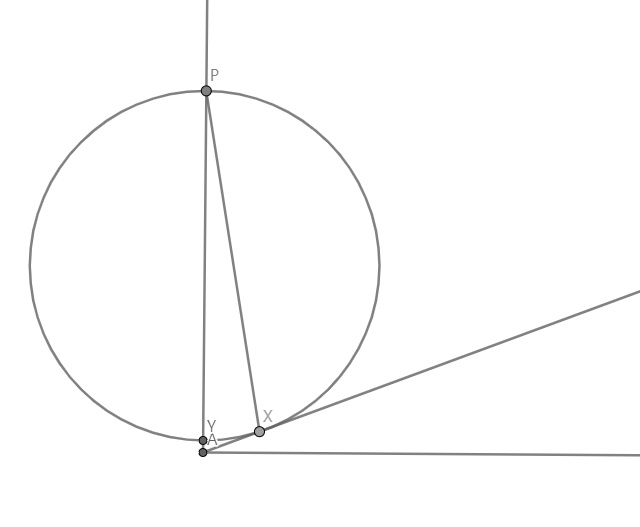
  이번엔 원의 중심이 선분 $\overline{PA}$ 위에 있고, $P$를 지나면서 경사와 접하는 원을 그려보았다. 이 경우 막대 $\overline{PX}$를 타고 내려가는 시간은 $P$에서 $Y$까지 자유낙하하는 시간과 같다. 이 그림에서 다른 모든 막대들을 그려보았을 때 이 시간보다 짧게 내려갈 수 있는 시간은 없다. 따라서 구하는 막대는 바로 $\overline{PX}$가 된다. 이제 계산해주는 일만 남았다.

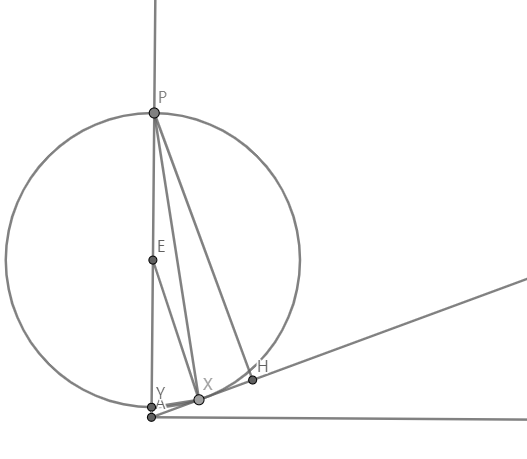
$H$ : |$P$에서 경사까지 내린 수선의 발|
$E$ : |$⊙PXY$의 중점|
$∠EPX = ∠EXP$ ($△PEX$ 이등변삼각형)
           $= ∠XPH (∠EXA =∠PHX=90˚⇔EX//PH)$
∴$\overline{PX}$는 $∠APH$의 이등분선
→ $∠XPH = \frac{1}{2}∠APH = \frac{1}{2}θ$

→ |막대의 길이 = $\overline{PX}$ = $\overline{PH} \sec{\frac{1}{2}θ} = h \cos\theta \sec\frac{1}{2}θ$
→ |막대의 길이| = $\frac{1}{2} g \cos\frac{1}{2}\theta$ |걸리는 시간|²
∴ |걸리는 시간| = $(\frac{2h\space\cos\theta}{g\space{\cos}^2 \frac{\theta}{2}})^{\frac{1}{2}}$

 

 이렇게 최소 시간과 길이를 구할 수 있다. 근데 여기까지만 하면 아쉽기 때문에 조금 더 일반화를 해보자.

 let) $Q∈AH, ∠GPH = x$
|막대 길이| = $L = \overline{PH} \sec x = h \cos θ \space\sec x$
|가속도| = $a = g \space\sin(\frac{\pi}{2} - (θ - x)) = g\space\cos(θ - x)$
$∴$ $t = {(\frac{2L}{a})}^{\frac{1}{2}} = {(\frac{2h cos θ}{g\space\cos x\space\cos(θ - x)})}^{\frac{1}{2}}$
$t$가 최소 $⇔ \cos x\space \cos(θ - x)$ 가 최대 (분모)
let) $f(x) = \cos x\space \cos(θ - x)$
$→\frac{\text{d}f(x)}{\text{d}x} = \sin x\space \cos(θ - x) + \cos x +(-1)(-\sin(θ - x))$
                 $= sin(θ - 2x)$
$∴ x =\frac{\theta}{2}$일 때 $f(x)$가 극대값을 가짐.
$→ \overline{PQ}$가 $∠APH$의 이등분선일 때 $t$가 최소

이렇게 함수를 만들어 미분을 이용하면 최소를 쉽게 구할 수도 있다.