티스토리 뷰
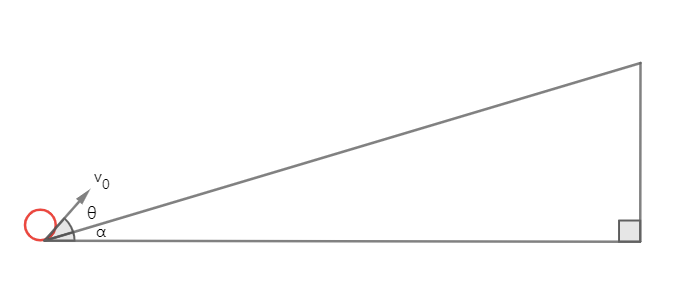
각 $α$만큼 기울어진 빗면에서 $θ$의 각도로 초속 $v_{0}$로 공을 던진다. 공의 출발 위치로부터 공아 밧면 위에 떨어진 지점까지의 거리가 최대가 되기 위한 $θ$와 이때의 최대 도달 거리를 구하여라.
이 문제를 풀기 위해 중력가속도와 초속를 빗면의 수직 성분과 수평 성분으로 분해해보자.

1. 빗면에 수직인 성분
빗면에 수직인 성분 관점에서 보면 초속도가 ${v_{0}}\space{\sin\theta}$ 이고 가속도가 ${-g}\space {\cos\alpha}$이다. 따라서 다시 빗면에 착지하기까지 걸리는 시간 $t$는 최고점까지 올라가는 시간의 2배이므로 아래와 같은 식이 성립한다.

2. 빗면에 수평인 성분
빗면에 수평인 성분 관점에서 보면 초속도가 ${v_{0}}\space{\cos\theta}$ 이고 가속도가 ${-g}\space{\sin\alpha}$ 이다. 운동을 $t$초동안 하므로 도달 거리를 $R$ 이라고 하면,

이러한 식이 나온다. 이제 이 값을 잘 계산해보자.
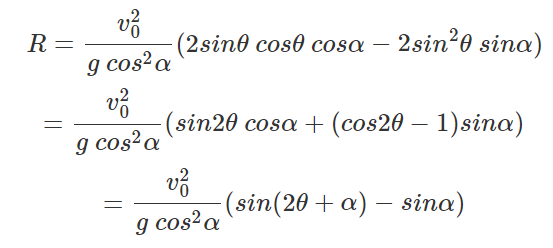
여기서
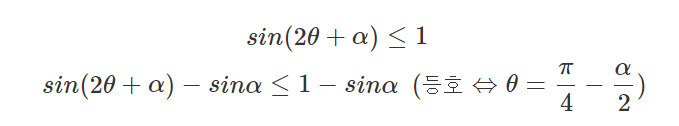
이므로,

이다.
따라서 $θ = 45º-\frac{\alpha}{2}$ 인 경우 $R$이 최대가 된다.
'Science > Physics' 카테고리의 다른 글
| 물체가 복사 평형에 도달하는데까지 걸리는 시간 (0) | 2024.05.11 |
|---|---|
| 공이 달린 막대가 회전하는 데까지 걸리는 시간 (꽤 어려움) (1) | 2024.04.03 |
| 물체를 경사로 떨어뜨리는데 걸리는 최소 시간 (1) | 2024.01.27 |
