티스토리 뷰
CSES. Stick Divisions
priority queue, greedy
입력으로 최종 상태의 분할 방법이 주어져있어서 분할하는 것보다 합치는 것으로 생각하는게 훨씬 편함. 길이 $l_1,l_2$인 두 막대를 합친다고 생각할 때 비용은 $l_1+l_2$이며 결과적으로 모든 막대를 합쳐야함. 이때 $N\leq 2\times 10^5$라서 $O(N\log_{}{N})$ 풀이가 필요함. 조금만 생각해보면 매순간마다 가장 작은 길이의 두 막대를 합치는 것이 비용적으로 최소임. 합치는 턴마다 막대가 1개씩 줄어드므로 $N$번 반복하면 되고 이때 최소인 두개를 찾는 것은 priority queue를 이용하면 $O(\log{}{N})$만에 할 수 있음.
#include <bits/stdc++.h>
#define fastio cin.tie(0)->ios::sync_with_stdio(0);
using namespace std;
int x,n;
priority_queue<int,vector<int>,greater<int>> pq;
void solve(){
int ans = 0;
while((int)pq.size() > 1){
int l1 = pq.top(); pq.pop();
int l2 = pq.top(); pq.pop();
ans += l1 + l2;
pq.push(l1+l2);
}
cout<<ans;
}
int main(){
fastio;
cin>>x>>n;
for(int i=0;i<n;i++){
int l; cin>>l;
pq.push(l);
}
solve();
}
USACO 2024 December. Deforestation
priority queue, greedy
처음에 접근할 때에는 자신이 포함되어있는 규제가 많은 나무들을 선택하려고 했었는데 구현도 복잡할 거 같고 시간복잡도도 상당할 것 같아서 금방 철회했다. 어떤 구간에서 제거할 수 있는 나무들의 개수 $cutNum$ 는 그 구간에 존재하는 모든 나무의 개수 $existing$와 최소한 필요한 나무의 개수 $t$의 차이이다. $($i.e. $cutNum = existing - t)$ 따라서 규제의 오른쪽 끝 $r_i$까지 제거한 나무의 최대 개수는 $l_i$이전까지 자른 나무의 개수 $a$와 $cutNum$의 합이다.
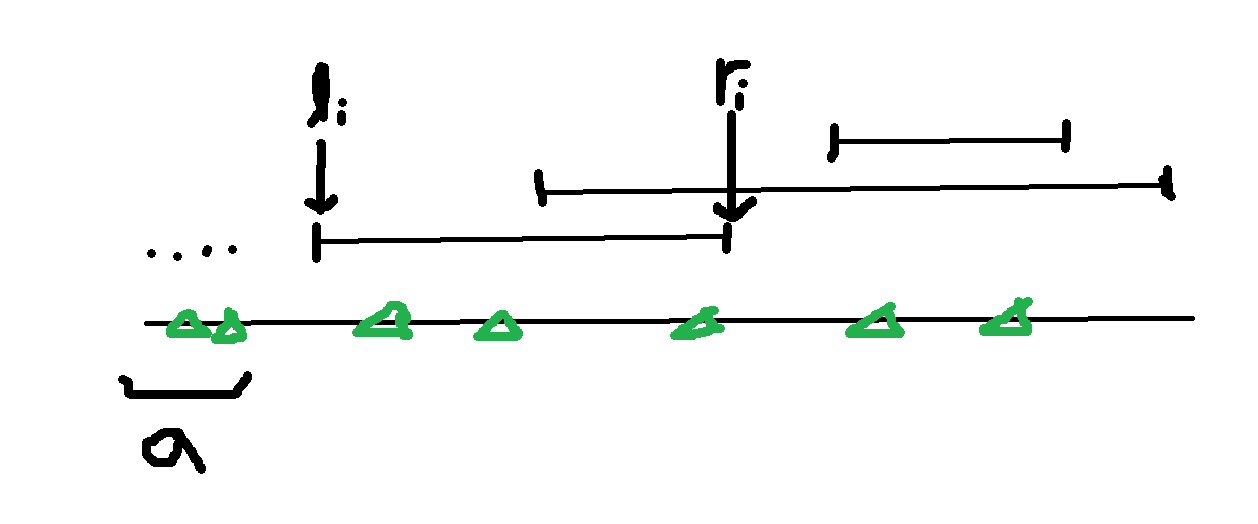
이를 효율적으로 처리하려면 priority queue에 현재 구간에서 적용되는 규제들을 $a+cutNum$을 기준으로 저장해놓으면 된다. 결과적으로 시간복잡도는 $O((N+K)\log{}{(N+K)})$이다. $N,K \leq 10^5$라서 가능하다.
#include <bits/stdc++.h>
using namespace std;
#define fastio cin.tie(0)->ios::sync_with_stdio(0);
typedef pair<int,int> pii;
const int NMAX = 1e5;
struct event{
int l,r,t,cutNum;
int c;
bool operator<(const event &e){
if(l == e.l) return c < e.c;
return l < e.l;
}
};
int N,K, x[NMAX + 10];
vector<event> events;
void solve(){
sort(events.begin(),events.end());
priority_queue<pii,vector<pii>,greater<pii>> pq;
int ans = 0;
for(event e : events){
if(e.c == -1){
pq.push({ans + e.cutNum, e.r});
} else {
while(!pq.empty() && pq.top().second < e.l) pq.pop();
if(pq.empty()){
ans ++;
} else {
pair<int,int> p = pq.top();
if(ans < p.first){
ans ++;
}
}
}
}
cout<<ans<<"\n";
}
int main(){
fastio;
int T; cin>>T;
while(T--){
cin>>N>>K;
for(int i=0;i<N;i++){
int loc; cin>>loc;
x[i] = loc;
events.push_back({loc,0,0,0,0});
}
sort(x,x+N);
for(int i=0;i<K;i++){
int l,r,t; cin>>l>>r>>t;
int existing = upper_bound(x,x+N,r) - lower_bound(x,x+N,l);
events.push_back({l,r,t,existing - t,-1});
}
solve();
events.clear();
}
}
BOJ 3197. 백조의 호수
union-find, simulation, bfs
메모리 초과가 조금 짜증났던 문제이다. $R,C \leq 1500 $이라서 문제에서 주어진 대로 시뮬레이션을 해주면 된다. 물과 맞닿아있는 얼음들을 queue나 vector에 넣어주고 매 순간마다 두 백조가 연결되어있는지를 확인하면 된다. 근데 이때 완전 brute force하게 탐색해버리면 $O(R^2 \times C^2)$이니 이건 안되고 union-find를 이용할 수 있다. 전체적인 시간복잡도는 얼음이 최대 $R\times C$개 만큼 있으므로 $O(RC \times \log{}{RC})$이다. 그런데 구현할 때 이미 녹았던 얼음들을체크를 안해주면 쓸데없는 얼음들도 계속 들어가 MLE를 받는다 ._. ,, 이를 신경써주며 구현하면 된다.
#include <bits/stdc++.h>
#define fastio cin.tie(0)->ios::sync_with_stdio(0);
using namespace std;
const int nmax = 1500*1500;
const int dx[4] = {0,0,1,-1}, dy[4] = {1,-1,0,0};
bool land[1510][1510], visited[1510][1510];
int parent[nmax+10],rk[nmax+10];
int R,C, ans = 0;
vector<int> swans;
int getparent(int a){
if(parent[a] == a) return a;
return parent[a] = getparent(parent[a]);
}
void unionparent(int a, int b){
a = getparent(a);
b = getparent(b);
if(a==b) return;
if(rk[a] < rk[b]){
parent[a] = b;
}
else{
parent[b] = a;
if(rk[a] == rk[b]) rk[a] ++;
}
}
void init(){
for(int i=0;i<=R*C;i++) {
parent[i] = i;
rk[i] = 0;
}
for(int i=0;i<R;i++){
for(int j=0;j<C;j++){
if(!land[i][j]) continue;
for(int d=0;d<4;d++){
int nr = i + dx[d];
int nc = j + dy[d];
if(nr < 0 || nc < 0 || nr >= R || nc >= C) continue;
if(land[nr][nc]) unionparent(i*C+j, nr*C+nc);
}
}
}
}
int main(){
fastio;
cin>>R>>C;
queue<pair<int,int>> melt;
for(int i=0;i<R;i++){
string ices; cin>>ices;
for(int j=0;j<C;j++){
if(ices[j] == '.') land[i][j] = true;
if(ices[j] == 'L'){
land[i][j] = true;
swans.push_back(C*i+j);
}
}
}
init();
for(int i=0;i<R;i++){
for(int j=0;j<C;j++){
if(land[i][j]) continue;
for(int d=0;d<4;d++){
int nr = i + dx[d];
int nc = j + dy[d];
if(nr < 0 || nc < 0 || nr >= R || nc >= C) continue;
if(land[nr][nc]) {
melt.push({i,j});
visited[i][j] = true;
break;
}
}
}
}
while(true){
if(getparent(swans[0]) == getparent(swans[1])){
cout<<ans<<"\n";
break;
}
ans ++;
int sz = melt.size();
for(int i=0;i<sz;i++){
int r = melt.front().first;
int c = melt.front().second;
melt.pop();
land[r][c] = true;
for(int d=0;d<4;d++){
int nr = r + dx[d];
int nc = c + dy[d];
if(nr < 0 || nc < 0 || nr >= R || nc >= C) continue;
if(land[nr][nc]){
if(getparent(nr*C+nc) == getparent(r*C+c)) continue;
unionparent(nr*C+nc, r*C+c);
} else {
if(!visited[nr][nc]) melt.push({nr,nc});
visited[nr][nc] = true;
}
}
}
}
}
KOI 2024. 색깔 모으기
union-find, permutation cycle decomposition
문제를 잘 관찰해보면 가능한 순열의 종류가 크게 두 가지임을 알 수 있다. 첫 번째는 모든 정점에서 모든 정점까지 경로가 존재하는 사이클과 out-degree가 2, in-degree가 2인 정점이 각각 하나씩 있는 DAG가 있다. 그렇지만 두 그래프 모두 어떤 정점에서 시작해 방향 간선을 따라 이동시키다보면 결국에는 $($구성원소 개수$) + 1$만큼의 시행으로 모두 크기 1짜리 기본 사이클로 바꿀 수 있다.
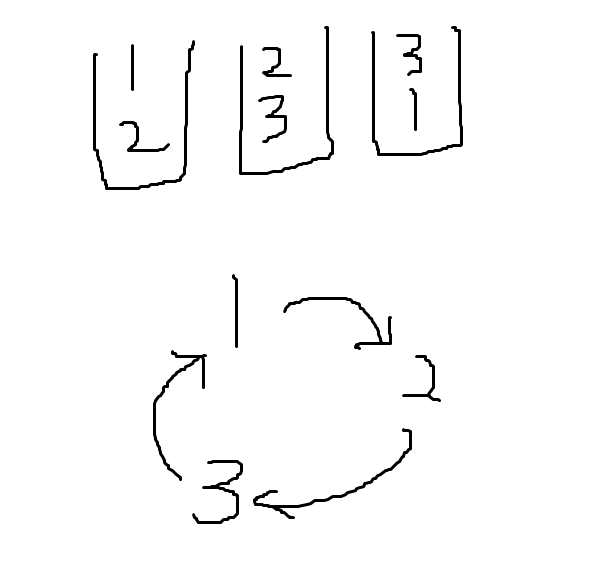

그래서 이런 종류에 속하는 서로 다른 분리 집합의 개수가 몇개인지를 세주면 되는데 이는 union-find를 이용해 log시간에 처리할 수 있다. 따라서 전체 시간복잡도는 $O(N\log{}{N})$으로 쓸 수 있다.
#include <bits/stdc++.h>
#define fastio cin.tie(0)->ios::sync_with_stdio(0);
using namespace std;
const int NMAX = 2e5;
int N, deletedNum = 0;
vector<int> A, B;
int outDeg[NMAX + 10], p[NMAX + 10], rk[NMAX + 10];
set<int> st, parents;
bool isDeleted[NMAX + 10];
int getParent(int a){
if(p[a] == a) return a;
return p[a] = getParent(p[a]);
}
void merge(int a, int b){
a = getParent(a); b = getParent(b);
if(a == b) return;
if(rk[a] > rk[b]) p[b] = a;
else {
if(rk[a] == rk[b]) rk[b] ++;
p[a] = b;
}
}
void solve(){
int cnt = 0;
for(int i=1;i<=N;i++){
if(isDeleted[i]) continue;
int parent = getParent(i);
auto iter = parents.find(parent);
if(iter == parents.end()){
cnt ++;
parents.insert(parent);
}
if(outDeg[i] >= 2) {
auto it = st.find(parent);
if(it != st.end()){
cout<<-1;
return;
}
st.insert(parent);
}
}
cout<<N + deletedNum + cnt;
}
int main(){
fastio;
cin>>N;
for(int i=0;i<=N;i++) p[i] = i;
for(int i=0;i<N;i++){
int a,b; cin>>a>>b;
if(a == b){
isDeleted[a] = true;
deletedNum --;
continue;
}
A.push_back(a); B.push_back(b);
outDeg[a] ++;
merge(a,b);
}
solve();
}'Computer Science' 카테고리의 다른 글
| PS Diary #6 (0) | 2025.01.16 |
|---|---|
| PS Diary #5 (1) | 2025.01.15 |
| PS Diary #4 (2) | 2025.01.02 |
| PS Diary #2 (1) | 2024.12.21 |
| PS Diary #1 (0) | 2024.12.20 |
