티스토리 뷰
KOI 2024. 이진트리
dp, math
문제는 상당히 어렵고 복잡할 것 같이 만들어놓고 풀어보면 진짜 별거없는 사기 문제이다. 그냥 $S(T)$ 들 간에 관계식을 잘 세워주면 풀린다. $T$의 왼쪽 자식의 서브트리를 $T_l$, 오른쪽 자식의 서브트리를 $T_r$이라고 하자. 또 T에 대해 T의 리프노드 개수가 $n$ 개일 때 $R(T) := \sum_{i=1}^{n}f(i,n)$, 그리고 $L(T) := \sum_{i=1}^{n}f(1,i)$로 정의하자. 일단 $S(T) = S(T_l) + S(T_r) + leafNum(T_l)\times L(T_r) + leafNum(T_r)\times R(T_l) - 1$ 임을 알 수 있다. $($설명하기에는 조금 복잡한데 대충 왼쪽만 쓸 때, 오른쪽만 쓸 때, 같이 쓸 때를 나눠서 더블카운팅으로 세주면 유도된다$)$. 또 $R(T) = R(T_r) + leafNum(T_l) - 1 + R(T_l)$ 이고, $L(T) = L(T_l) + leafNum(T_r) - 1 + L(T_r)$로 쓸 수 있다. 이를 계속 계산해주면 $O(N)$만에 풀린다. 그리고 점화식들간의 관계가 다 합이랑 곱밖에 없어서 그냥 모듈러 연산도 너무 쉽게 된다. 솔직히 플레티넘 4 난이도는 아닌거 같다는 생각이 들었다.
#include <bits/stdc++.h>
#define fastio cin.tie(0)->ios::sync_with_stdio(0);
using namespace std;
typedef long long ll;
const ll MOD = 1e9 + 7;
const int NMAX = 1e5;
int N;
ll RightNum[NMAX + 10], LeftNum[NMAX + 10];
ll S[NMAX + 10], leafNum[NMAX + 10];
int main(){
fastio;
cin >> N;
S[0] = RightNum[0] = LeftNum[0] = leafNum[0] = 1;
for(int i=1;i<=N;i++){
int r,l; cin >> l >> r;
S[i] = (S[l] + S[r] + (leafNum[l]*LeftNum[r])%MOD + (leafNum[r]*RightNum[l])%MOD - 1) % MOD;
leafNum[i] = (leafNum[l] + leafNum[r]) % MOD;
RightNum[i] = (RightNum[r] + leafNum[l] - 1 + RightNum[l]) % MOD;
LeftNum[i] = (LeftNum[l] + leafNum[r] - 1 + LeftNum[r]) % MOD;
cout << S[i] << "\n";
}
}
BOJ 2612. DNA 유사도
dp
정올 사이트에서 단계별 문제 구경하다가 재밌게 생겨서 풀어봤다. 처음보자마자 든 생각은 $O(N^2)$ 으로 LCS구하는 것처럼 dp table 채우는 방식으로 해야겠다고 생각했다. 문자열 S1, S2에 대해서 $dp[i][j] := (S1[i], S2[j]$ 를 마지막으로 포함할 때의 최대 점수$)$로 정의하면 잘 풀린다. 점화식 관계는 크게 이전 문자열들을 안 쓸 때와 이전 문자열들을 쓸 때로 나누고, 이전 문자열들을 쓸 때에서 또 빈칸 쓸 때와 빈칸 안쓸 때로 나누어서 생각하면 쉽게 얻을 수 있다. $$\delta _{i,j} = \begin{cases}3 & i = j\\-2 & i \not =j\end{cases}$$이라고 할 때 $dp[i][j] = \max(\delta_{i,j},\space dp[i-1][j]-2,\space dp[i][j-1] -2,\space dp[i-1][j-1]+\delta_{i,j})$라는 예쁘지 않은 식을 얻을 수 있다. 이제 실례를 출력해줘야하는데 처음부터 $dp[i][j]$에 문자열까지 저장하면 문자열의 최대 길이가 $N$이므로 공간복잡도가 $O(N^3)$이라서 128MB를 초과할 수밖에 없다. 따라서 이전 인덱스만 저장해주고 나중에 역추적하는 방식으로 짜야한다. 시간복잡도는 $O(N^2)$이다.
#include <bits/stdc++.h>
#define fastio cin.tie(0)->ios::sync_with_stdio;
using namespace std;
typedef pair<int,int> pii;
const int NMAX = 1e3;
struct info {
int value;
pii bef;
};
int N, M;
info dp[NMAX + 10][NMAX + 10];
string base1, base2;
void solve() {
int ans = -99999; pii ansPair;
dp[0][0].value = (base1[0] == base2[0]) ? (3) : (-2);
dp[0][0].bef = {0,0};
for (int i = 0; i < N; i++) {
for (int j = 0; j < M; j++) {
if (i == 0 && j == 0) continue;
int v = (base1[i] == base2[j]) ? (3) : (-2);
pii Bef = {i,j};
if (i >= 1) {
if (v < dp[i - 1][j].value - 2) {
v = dp[i - 1][j].value - 2;
Bef = {i-1,j};
}
}
if (j >= 1) {
if (v < dp[i][j - 1].value - 2) {
v = dp[i][j - 1].value - 2;
Bef = {i,j-1};
}
}
if (i >= 1 && j >= 1) {
if (base1[i] == base2[j]) {
if (v < dp[i - 1][j - 1].value + 3) {
v = dp[i - 1][j - 1].value + 3;
Bef = {i-1,j-1};
}
} else {
if (v < dp[i - 1][j - 1].value - 2) {
v = dp[i - 1][j - 1].value - 2;
Bef = {i-1,j-1};
}
}
}
dp[i][j] = {v, Bef};
if (ans < v) {
ans = v;
ansPair = {i,j};
}
}
}
cout << ans << "\n";
pii x = ansPair;
stack<int> st1, st2;
st1.push(x.first); st2.push(x.second);
while(true){
if(x.first == dp[x.first][x.second].bef.first && x.second == dp[x.first][x.second].bef.second) break;
x = dp[x.first][x.second].bef;
if(st1.top() != x.first) st1.push(x.first);
if(st2.top() != x.second) st2.push(x.second);
}
while(!st1.empty()){
cout << base1[st1.top()];
st1.pop();
} cout << "\n";
while(!st2.empty()){
cout << base2[st2.top()];
st2.pop();
}
}
int main() {
fastio;
cin >> N >> base1;
cin >> M >> base2;
solve();
}
CodeForces Round 828. MEX vs MED
math, two pointer
Div. 3의 F번인데 푸는데 꽤 시간이 많이 걸렸다. $mex(p_l,p_{l+1}...,p_r)$ $>$ $med(p_l,p_{l+1}...,p_r)$ 라는 조건을 만족시키기 위한 조건이 무엇인지를 고민해보면 $p_l, ... , p_r$ 까지 숫자가 $k = l-r+1$ 개 있으므로 $med(p_l,p_{l+1}...,p_r)$ 은 최소한 $\lfloor\frac{k-1}{2}\rfloor$ 보단 크거나 같으므로 $mex(p_l,p_{l+1}...,p_r)$ 도 적어도 $\lfloor\frac{k-1}{2}\rfloor$ 보단 커야한다. 이때는 $p_l, ... , p_r$ 에 0부터 $\lfloor\frac{k-1}{2}\rfloor$ 가 모두 포함되어있다는 말이다. 또한 이 조건을 만족시키면 $med(p_l,p_{l+1}...,p_r)$ $=$ $\lfloor\frac{k-1}{2}\rfloor$ 이고, $med(p_l,p_{l+1}...,p_r)$ $>$ $\lfloor\frac{k-1}{2}\rfloor$ 이므로 필요충분 조건이 된다. 여기까지 알았어도 고민해야할게 좀 더 남아있다. $X[k] := (0$부터 $k$까지를 모두 포함하고 $k-1$은 포함하지 않고, 문제의 조건을 만족시키는 subsegment의 개수$)$ 라고 정의하자. 정의에 따라 구하는 정답은 $\sum_{k=0}^{n-1}X[k]$ 이 된다. $0 \leq k < n$ 에 대해 $X[k]$를 $O(1)$으로 계산할 수 있으면 $O(N)$ 풀이가 완성된다. 구하는 방법은 0부터 $k$를 모두 포함하는 최소 구간에 대해 그 구간의 최소 인덱스와 최대 인덱스와 $k+1$의 위치를 이용하여 계산할 수 있다. 이 과정을 인덱스를 '확장'한다고 표현하자. 각각의 인덱스를 확장할 수 있는 제약조건은 $k+1$의 위치와 $0,n-1$ 내부에 존재해야한다는 것과 전체 길이가 $2\times k + 2$보다는 작아야한다는 것을 통해 쓸 수 있다.
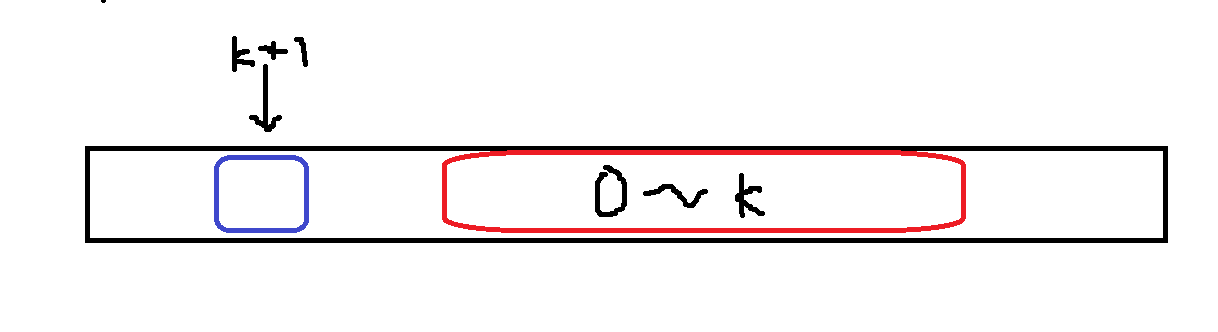
따라서 다음과 같은 수학문제와 동일하다.
$0\leq x \leq m$ 이고,$ 0\leq y \leq n$ 인 정수 $x,y$에 대해 $x + y \leq c$ 를 만족시키는 $(x,y)$의 개수는?
이건 생각을 잘해보면 계산식을 만들 수 있으므로 $O(1)$ 만에 계산할 수 있다. 따라서 전체적인 시간복잡도는 $O(N)$이 된다.
#include <bits/stdc++.h>
#define fastio cin.tie(0)->ios::sync_with_stdio(0);
using namespace std;
const int NMAX = 2e5;
typedef long long ll;
ll n, indices[NMAX + 10];
void solve(){
ll ans = 1;
ll mxIdx = 0, mnIdx = n;
for(ll i=0;i<n-1;i++){
mxIdx = max(mxIdx, indices[i]);
mnIdx = min(mnIdx, indices[i]);
if(indices[i+1] >= mnIdx && indices[i+1] <= mxIdx) continue;
ll canExpand = 2*i+2 - (mxIdx-mnIdx+1), canExpandF,canExpandB;
if(canExpand < 0) continue;
if(indices[i+1] > mxIdx){
canExpandF = min(indices[i+1]-mxIdx-1,canExpand);
canExpandB = min(mnIdx,canExpand);
} else {
canExpandF = min(n-mxIdx-1,canExpand);
canExpandB = min(mnIdx - indices[i+1] - 1,canExpand);
}
if(canExpandF <= canExpand - canExpandB){
ans += (canExpandB + 1)*(canExpandF + 1);
} else {
ans += (canExpandF + 1)*(canExpand - canExpandF + 1);
ans +=(canExpandF + canExpandB - canExpand)*(canExpandF+canExpand-canExpandB+1)/2;
}
}
cout << ans << '\n';
}
int main(){
fastio;
int T; cin >> T;
while (T --){
cin >> n;
for(ll i=0;i<n;i++) {
int p; cin >> p;
indices[p] = i;
}
solve();
}
}
BOJ 13976. 타일 채우기 2
exponentiation by squaring, math
일단 $N$이 홀수인 경우는 불가능함이 당연하므로 짝수인 경우에서만 고려하자. $N = 2k$일 때 구하는 경우의 수를 $a_k$라고 하자. 초기에 앞을 꽉 채울 수 있는 방법들을 생각해보면 아래와 같은 방법들이 있다. 여기서 맨 위의 경우는 2칸을 줄일 수 있고 나머지 경우들을 짝수 칸씩 줄일 수 있으며 위 아래를 바꿀 경우 한 가지 경우가 더 있다.

따라서 점화식을 세워보면 $a_k = a_{k-1} + 2\sum_{i=0}^{k-1} a_{i}$ 와 같이 쓸 수 있다. 이를 조금 변형하면 $a_k = 4a_{k-1} - a_{k-2}$라는 인접삼항간 점화식이 된다. 이제 이걸 계산해주면 되는데 $N \leq 10^{18}$ 이라 $O(N)$으로는 안되고 피보나치를 구할 때처럼 분할정복을 활용해야한다. 행렬을 찾아서 거듭제곱 해도 되지만 나는 일반식을 세우고 $a+b\sqrt{3}$ 형태의 무리수를 이용하여 풀었다. $a_k = \frac{(2+\sqrt{3})^k(1+\sqrt{3})+(2-\sqrt{3})^k(\sqrt{3}-1)}{2\sqrt{3}}$ 이므로 무리수 거듭제곱만 잘 계산해주면 된다. 마지막에서 $2\sqrt{3}$ 으로 나누는 부분에서는 $10^9 + 7$에 대한 모듈러 연산을 해야하므로 2의 모듈러 역원인 $5\times 10^8 + 4$ 를 곱해주었다.
#include <bits/stdc++.h>
#define fastio cin.tie(0)->ios::sync_with_stdio(0);
using namespace std;
typedef long long ll;
const ll MOD = 1e9 + 7;
struct irrat {
ll a, b; //a + b sqrt(3)
};
ll N;
irrat alpha1 = {2, -1}, alpha2 = {2, 1};
irrat beta1 = {1,1}, beta2 = {-1,1};
irrat multi(irrat i1, irrat i2) {
irrat rtv;
rtv.a = ((i1.a * i2.a) % MOD + (3 * i1.b * i2.b) % MOD) % MOD;
rtv.b = ((i1.a * i2.b) % MOD + (i1.b * i2.a) % MOD) % MOD;
return rtv;
}
irrat add(irrat i1, irrat i2) {
irrat rtv;
rtv.a = (i1.a + i2.a) % MOD;
rtv.b = (i1.b + i2.b) % MOD;
return rtv;
}
irrat pow(irrat i, ll p) {
if(p == 1) return i;
if(p % 2 == 0) {
irrat half = pow(i,p/2);
return multi(half, half);
} else {
irrat half = pow(i,p/2);
return multi(i,multi(half, half));
}
}
void solve() {
if(N % 2 == 1) cout << 0;
else {
N /= 2;
irrat I1 = multi(pow(alpha2,N),beta1);
irrat I2 = multi(pow(alpha1,N),beta2);
irrat ans = add(I1, I2);
cout << (ans.b * 500000004) % MOD;
}
}
int main() {
fastio;
cin >> N;
solve();
}
CodeForces Round 998. Multiplicative Array
math, combinatorics, dp, number theory
이 문제를 실제 대회에서는 깊게 고민하지 않고 그냥 넘어갔었는데 다시 풀어보니 풀이가 재미있는 것 같다. 약간의 수학지식이 필요한 문제이다. 가장 중요했던 아이디어는 dp를 하는데 이때 1을 배제하고 해야한다는 것이다. $dp[i][x] := (2$ 이상 자연수 $i$개를 곱하여 $x$가 되는 순서쌍 개수$)$ 라고 정의하자. $2^{20} > 10^5$ 이므로 $i$의 최댓값은 적어도 20보다는 작다. 따라서 dp table이 2D이긴 하지만 $i \sim 10$이므로 사실상 1D이다. dp table을 채우는 것은 각 $i,x$ 와, $x*y \leq K$를 만족하는 모든 2이상 자연수 $y$에 대해 $dp[i+1][x*y] += dp[i][x]$를 해주면 된다. $2\leq y \leq \frac{K}{x}$ 이므로 전체 연산횟수는 $\sum_{y=2}^{x}\frac{K}{y} = K\sum_{y=2}^{x}\frac{1}{y} \approx K\ln{}{x}$ 이므로 시간복잡도는 $O(K\log{}{K})$가 된다. 여기까지 했으면 1을 채우는 경우만 고려해주면 된다. 길이가 $l$ 인 수들 사이 사이에 1을 넣는 가짓수는 $ \sum_{k=0}^{n-l} (_{l+1}H_k) = \sum_{k=0}^{n-l} \binom{l+k}{k} = \binom{n+1}{l} $ 이므로 곱이 $x$인 순서쌍의 개수는 $\sum_{k=1}^{20} \binom{n+1}{k} dp[k][x]$ 이 된다. 추가적으로 998244353에 대한 나머지를 출력해야하므로 이항계수를 구할 때 모듈러 역원을 곱해줘야하는데 분할정복을 이용한 거듭제곱으로 모듈러 역원을 구했다.
#include <bits/stdc++.h>
#define fastio cin.tie(0)->ios::sync_with_stdio(0);
using namespace std;
typedef long long ll;
const ll MOD = 998244353;
const int KMAX = 1e5;
ll N, K;
ll dp[30][KMAX + 10], combination[30];
ll fastPow(ll num, ll p){
if(p == 1) return num;
ll half = fastPow(num,p/2);
if(p % 2 == 0) return (half*half)%MOD;
else return (num*((half*half)%MOD))%MOD;
}
void init(){
for(int l=0;l<30;l++)
for(int x=0;x<=K;x++)
dp[l][x] = 0;
for(int x=2;x<=K;x++) dp[1][x] = 1;
combination[0] = 1;
for(int l=1;l<30;l++){
combination[l] = (combination[l-1] * (N+2-l))%MOD;
combination[l] = (combination[l] * fastPow(l, MOD - 2))%MOD;
}
}
void solve(){
init();
for(int l=1;l<29;l++){
for(ll x=2;x<=K;x++){
for(ll y=2;y<=K/x;y++){
dp[l+1][x*y] += dp[l][x];
dp[l+1][x*y] %= MOD;
}
}
}
for(int x=1;x<=K;x++){
if(x == 1){cout << N << ' '; continue;}
ll ans = 0;
for(int l=1;l<29;l++){
ans += dp[l][x] * combination[l+1];
ans %= MOD;
}
cout << ans << ' ';
}
cout << '\n';
}
int main(){
fastio;
int t; cin >> t;
while(t--){
cin >> K >> N;
solve();
}
}'Computer Science' 카테고리의 다른 글
| PS Diary #8 (2) | 2025.02.16 |
|---|---|
| PS Diary #7 (4) | 2025.01.23 |
| PS Diary #5 (1) | 2025.01.15 |
| PS Diary #4 (2) | 2025.01.02 |
| PS Diary #3 (1) | 2024.12.26 |
