티스토리 뷰
BOJ 2517. 달리기
segment tree, coordinate compression
보자마자 세그먼트 트리가 떠올라야하는 문제이다. 어떤 선수의 최소 등수는 $($그 선수 앞에 있는 선수들 중 그 선수보다 실력이 좋은 선수들 명수$) + 1$ 등이 된다. 그래서 앞에서 부터 segment tree에 업데이트 해주며 계산해주면 된다. 또한 선수들 실력의 절대적인 값은 중요하지 않으므로 좌표 압축을 해주어야한다. 시간복잡도는 $O(N\log{}{N})$이다.
#include <bits/stdc++.h>
#define fastio cin.tie(0)->ios::sync_with_stdio(0);
using namespace std;
const int NMAX = 5e5;
int N;
vector<int> skill_level, cmp;
struct SegmentTree {
int n;
vector<long long> tree;
SegmentTree(int size) {
n = size;
tree.resize(4 * n);
}
void build(const vector<int>& arr, int node, int start, int end) {
if (start == end) {
tree[node] = arr[start];
} else {
int mid = (start + end) / 2;
build(arr, node * 2, start, mid);
build(arr, node * 2 + 1, mid + 1, end);
tree[node] = tree[node * 2] + tree[node * 2 + 1];
}
}
void update(int node, int start, int end, int idx, int val) {
if (start == end) {
tree[node] = val;
} else {
int mid = (start + end) / 2;
if (idx <= mid)
update(node * 2, start, mid, idx, val);
else
update(node * 2 + 1, mid + 1, end, idx, val);
tree[node] = tree[node * 2] + tree[node * 2 + 1];
}
}
long long query(int node, int start, int end, int l, int r) {
if (r < start || end < l) return 0;
if (l <= start && end <= r) return tree[node];
int mid = (start + end) / 2;
return query(node * 2, start, mid, l, r) + query(node * 2 + 1, mid + 1, end, l, r);
}
void build(const vector<int>& arr) {
build(arr, 1, 0, n - 1);
}
void update(int idx, int val) {
update(1, 0, n - 1, idx, val);
}
long long query(int l, int r) {
return query(1, 0, n - 1, l, r);
}
};
void solve(){
vector<int> st;
for(int s : skill_level) st.push_back(s);
sort(st.begin(), st.end());
for(int i=0;i<N;i++){
int idx = lower_bound(st.begin(), st.end(), skill_level[i]) - st.begin();
cmp.push_back(idx);
}
vector<int> isExist(N, 0);
SegmentTree seg(N);
seg.build(isExist);
for(int s : cmp){
seg.update(s, 1);
if(s != N-1) cout << seg.query(s+1, N-1) + 1 << "\n";
else cout << 1 << "\n";
}
}
int main(){
fastio;
cin >> N;
skill_level = vector<int> (N);
for(int &s : skill_level) cin >> s;
solve();
}
USACO December 2019. Moortal Cowmbat
floyd-warshall, dp, prefix sum
발상이 크게 어렵지 않으면서 쓰는 알고리즘이 많아서 재밌게 풀었던 문제이다. 처음에 당연히 해야할 행동은 각 알파벳에서 각 알파벳으로 바꾸는 최소 비용을 구하는 작업이다. 문제에서 아예 $a_{i,j}$ 형태로 입력이 주어졌으므로 floyd-warshall로 최소 거리를 업데이트 해줘야겠다는 생각은 금방 할 수 있다. 알파벳 개수가 26개 이하이므로 3제곱의 시간복잡도를 가져도 상관없다. 그 이후에는 뭔가 dp를 써야할 것만 같은 느낌이 나므로 dp table을 정의할 생각을 할 수 있다. $dp[i][j] := (i-1$ 번째 인덱스가 $j$번째 알파벳이고, 바로 직전까지 $j$번째 알파벳을 연속하게 $K$개 이상 썼을 때 최소 비용$)$ 와 같이 정의해보자. $dp[i][j]$ 를 채울 때 두 가지 경우가 있다. $i-1$ 번 까지 $j$번 알파벳이 채워져 있고 $i$ 번도 $j$ 번째 알파벳으로 채우는 경우와 $i-K$ 번까지 다른 알파벳으로 채워져있고 $i-K+1$ 부터 $i$까지 알파벳 $j$로 채우는 경우이다. 두 가지 경우 중에서 최솟값으로 $dp[i][j]$ 를 업데이트 해야하는데 두 번째 경우에서 그냥 계산하면 $O(K)$가 걸리므로 시간초과가 날 것이다. 따라서 두 번째 경우에서 알파벳을 바꿀 때 드는 비용을 prefix sum으로 미리 저장해놓고 계산해야한다. $prefix[i][j] := ($ 주어진 문자열에서 $0$부터 $i$ 번째 문자를 모두 $j$ 번째 알파벳으로 바꿀 때 드는 비용 $)$ 와 같이 정의하면 $O(NM)$에 채울 수 있다. 그러면 $dp[i][j]$는 $\min_{w\leq M, w \neq j}{(dp[i-K][w] + prefix[i][j] - prefix[i-K][j])}$ 와 $dp[i][j] = dp[i-1][j] + dist[combo[i-1]-'a'][j]$ 중 최솟값이다. 시간복잡도는 $O(NM + M^3)$ 이다.
#include <bits/stdc++.h>
#define fastio cin.tie(0)->ios::sync_with_stdio(0);
using namespace std;
const int MMAX = 26, NMAX = 1e5, INF = 1e9;
int N,M,K;
string combo;
int dist[MMAX + 10][MMAX + 10];
int prefix[NMAX + 10][MMAX + 10];
int dp[NMAX + 10][MMAX + 10];
void floyd(){
for(int k=0;k<M;k++)
for(int i=0;i<M;i++)
for(int j=0;j<M;j++)
dist[i][j] = min(dist[i][j], dist[i][k] + dist[k][j]);
for(int i=1;i<=N;i++)
for(int k=0;k<M;k++)
prefix[i][k] = prefix[i-1][k] + dist[combo[i-1]-'a'][k];
}
void solve(){
floyd();
for(int i=0;i<=N;i++)
for(int j=0;j<M;j++)
dp[i][j] = (i == 0) ? 0 : INF;
int ans = INF;
for(int i=K;i<=N;i++){
for(int j=0;j<M;j++){
dp[i][j] = dp[i-1][j] + dist[combo[i-1]-'a'][j];
for(int w=0;w<M;w++){
if(w == j) continue;
dp[i][j] = min(dp[i][j], dp[i-K][w] + prefix[i][j] - prefix[i-K][j]);
}
if(i == N) ans = min(ans, dp[i][j]);
}
}
cout << ans;
return;
}
int main(){
fastio;
cin >> N >> M >> K;
cin >> combo;
for(int i=0;i<M;i++)
for(int j=0;j<M;j++)
cin >> dist[i][j];
solve();
}
USCAO December 2018. Fine Dinning
dijkstra
그냥 다익스트라 문제인데 아이디어가 신박했다. 주요 아이디어는 haybale 이 있는 pasture을 지날 때 yumminess 만큼 비용이 줄어든다고 생각하는 것이다. 즉 그 pasture에 새로운 간선을 추가하는데 그 간선이 $($원래 그곳으로 가는 비용$)$ $-($yumminess$)$만큼의 가중치를 가졌다고 생각하는 것이다. 근데 값이 음수가 될 경우 dijskstra algorithm이 제대로 작동할 일이 없기도 하고, 반드시 저 간선을 지날 것이라는 보장이 없기 때문에 단순히 이렇게 해서는 답이 나오지 않는다. 그래서 새로운 정점을 추가해서 그 정점을 기준으로 dijkstra를 하는데 그 정점으로부터 나오는 간선이 방향 간선이라서 반드시 한번 지나도록 해주면 된다. 즉 $N+1$번째 정점을 추가해서 haybale을 가진 pasture과 연결되는 방향간선을 추가해주는데 그 가중치가 $(N$ 번째 정점에서 원래 그곳으로 가는 비용$)$ $-($yumminess$)$ 이 되는 것이다. 결과적으로 이렇게 구한 거리가 원래 거리보다 작거나 같은 경우 1을, 큰 경우 0을 출력해주면 된다. 시간복잡도는 그냥 다익스트라 시간복잡도와 동일하다.
#include <bits/stdc++.h>
#define fastio cin.tie(0)->ios::sync_with_stdio(0);
using namespace std;
typedef long long ll;
typedef pair<ll, ll> pll;
const int NMAX = 5e4;
const ll INF = 1e10;
ll N,M,K, h[NMAX + 10][2];
vector<pll> graph[NMAX + 10];
vector<ll> dijkstra(ll S){
vector<ll> rtv(N+2, INF);
priority_queue<pll, vector<pll>, greater<pll>> pq;
pq.push({0,S}); rtv[S] = 0;
while(!pq.empty()){
auto [cdist, cur_node] = pq.top(); pq.pop();
if(cdist != rtv[cur_node]) continue;
for(int i=0;i<graph[cur_node].size();i++){
ll nx_node = graph[cur_node][i].first;
ll ndist = graph[cur_node][i].second;
if(ndist + cdist < rtv[nx_node]){
pq.push({rtv[nx_node] = ndist + cdist, nx_node});
}
}
}
return rtv;
}
void solve(){
vector<ll> origin_dist = dijkstra(N);
for(int i=0;i<K;i++){
graph[N+1].push_back({h[i][0], origin_dist[h[i][0]]-h[i][1]});
}
vector<ll> new_dist = dijkstra(N+1);
for(int i=1;i<N;i++){
cout << (origin_dist[i] >= new_dist[i]) << "\n";
}
}
int main(){
fastio;
cin >> N >> M >> K;
for(int i=0;i<M;i++){
int a,b,w; cin >> a >> b >> w;
graph[a].push_back({b,w});
graph[b].push_back({a,w});
}
for(int i=0;i<K;i++){
cin >> h[i][0] >> h[i][1];
}
solve();
}
USACO US Open Contest 2018. Milking Order
binary search, topology sort
$k$번 째 순서까지 지킬 수 있으면 $k-1$번 째 순서까지 지킬 수 있음이 당연하다. 따라서 순서에 대한 이분탐색을 생각해볼 수 있고, 가능한 최대 순서를 출력하면 된다. $k$번 째 순서까지 만족시킬 수 있는지를 판단하는 것은 그냥 위상 정렬을 해보면 된다. 발상도 쉽고 구현도 쉬웠다. 시간복잡도는 $O(M\log{}{M}\log{}{N})$ 이다.
#include <bits/stdc++.h>
#define fastio cin.tie(0)->ios::sync_with_stdio(0);
using namespace std;
const int NMAX = 1e5;
int N,M;
vector<int> ord[NMAX + 10];
vector<int> topSort(int x){
vector<vector<int>> graph(N+1);
vector<int> inDeg(N+1, 0), rtv;
for(int i=0;i<=x;i++){
for(int j=0;j<ord[i].size()-1;j++){
graph[ord[i][j]].push_back(ord[i][j+1]);
inDeg[ord[i][j+1]] ++;
}
}
priority_queue<int, vector<int>, greater<int>> pq;
for(int i=1;i<=N;i++)
if(inDeg[i] == 0)
pq.push(i);
while(!pq.empty()){
int v = pq.top();
pq.pop(); rtv.push_back(v);
for(int i=0;i<graph[v].size();i++){
int u = graph[v][i];
if(--inDeg[u] == 0) pq.push(u);
}
}
return rtv;
}
void solve(){
int l=0, r=M-1, ans=0;
while(l <= r){
int mid = (l+r)/2;
if(topSort(mid).size() == N){
ans = max(ans, mid);
l = mid + 1;
} else r = mid - 1;
}
vector<int> final_order = topSort(ans);
for(int x : final_order) cout << x << " ";
}
int main(){
fastio;
cin >> N >> M;
for(int i=0;i<M;i++){
int m; cin >> m;
ord[i] = vector<int>(m);
for(int &x : ord[i]) cin >> x;
}
solve();
}
USACO January 2025. Farmer John's Favorite Operation
math, sort, prefix sum, binary search
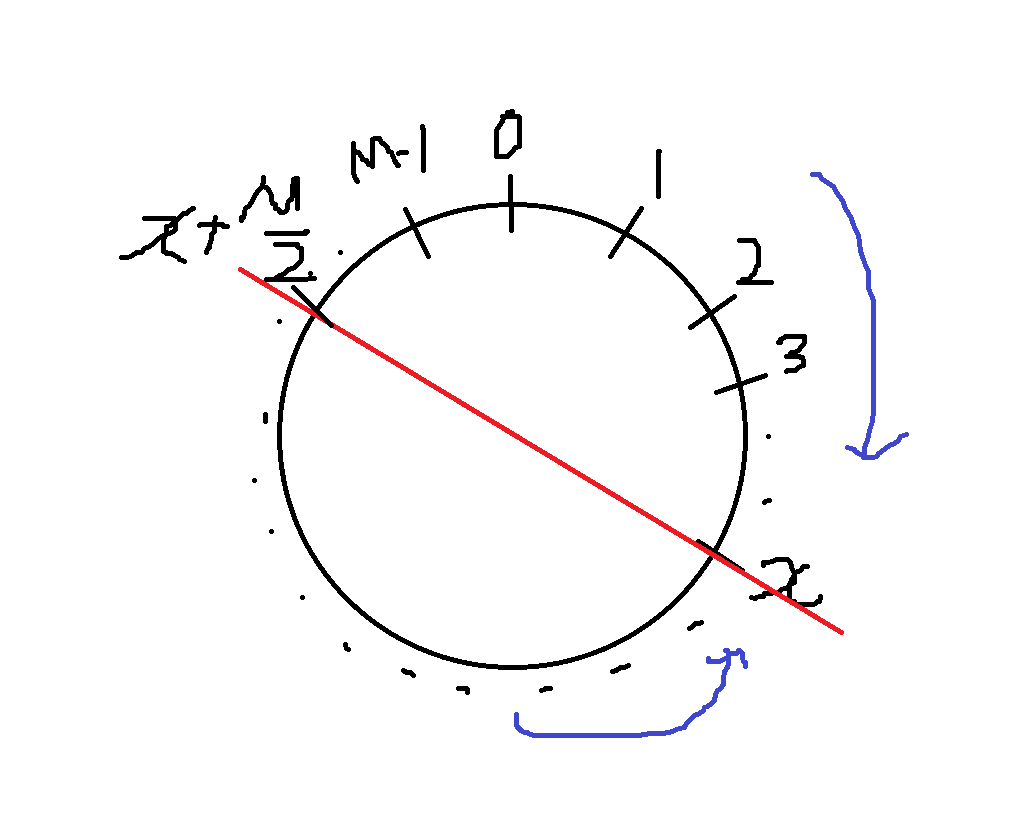
1월에 기출되었던 문제인데 실제 대회에서 빨리 풀었었다. 완전 수학 문제였는데 배열의 모든 숫자를 modulo $M$에 대해 모두 합동이도록 만들기 위해 필요한 최소 연산 횟수를 구하면 된다. modulo $M$ 에서 가능한 숫자는 $0$부터 $M-1$까지 $M$개가 있으므로 탐색공간이 많다. 그래서 탐색공간을 줄이기 위해 생각을 해보다 보면 굳이 $M$개를 탐색할 필요없이 배열에 존재하는 숫자 내에서만 탐색해도 충분하다는 것을 알 수 있다. 연산횟수는 $M$개의 숫자가 써져있는 원탁에서 최소거리와 같다. 대척점을 기준으로 어느방향이 최소인지 알 수 있다. 이를 이분탐색과 누적합을 이용하면 쉽게 계산할 수 있다.
#include <bits/stdc++.h>
#define fastio cin.tie(0)->ios::sync_with_stdio(0);
using namespace std;
typedef long long ll;
typedef pair<ll,ll> pii;
const int NMAX = 5e5;
ll N,M,a[NMAX + 10],prefix[NMAX + 10];
void solve(){
ll ans = 1e18;
sort(a,a+N);
for(int i=1;i<=N;i++){
prefix[i] = prefix[i-1] + a[i-1];
}
for(int i=0;i<N;i++){
ll value = 0;
ll std1 = (2*a[i] - M)/2, std2 = (2*a[i] + M)/2;
if(a[0] >= std1){
ll idx1 = upper_bound(a,a+N,a[i]) - a; idx1 --;
value += a[i]*(idx1+1) - prefix[idx1+1];
ll idx2 = upper_bound(a,a+N,std2) -a; idx2 --;
value += prefix[idx2+1] - prefix[idx1+1] - a[i]*(idx2-idx1);
value += (M+a[i])*(N-1-idx2)- prefix[N] + prefix[idx2+1];
} else {
ll idx = upper_bound(a,a+N,std1) -a; idx --;
value += prefix[idx+1] - (idx+1)*(a[i]-M);
ll idx1 = upper_bound(a,a+N,a[i]) - a; idx1 --;
value += a[i]*(idx1-idx) - prefix[idx1+1] + prefix[idx + 1];
ll idx2 = upper_bound(a,a+N,std2) -a; idx2 --;
value += prefix[idx2+1] - prefix[idx1+1] - a[i]*(idx2-idx1);
value += (M+a[i])*(N-1-idx2)- prefix[N] + prefix[idx2+1];
}
ans = min(ans, value);
}
cout << ans << '\n';
}
int main(){
fastio;
int T; cin >> T;
while(T--){
cin >> N >> M;
for(int i=0;i<N;i++) {
cin >> a[i];
a[i] %= M;
}
solve();
}
}
USACO January 2025. Cow Checkups
math, binary search, prefix sum
이 문제도 실제 대회에서 풀었던 문제이다. 나만 복잡하게 푼 건지는 모르겠지만 완전 수학적으로 풀어서 구현이 까다로웠었다. 문제를 푼지 시간이 꽤 지나서 풀이를 자세히 쓰기는 귀찮다$($ㅎㅎ$)$. 대충 설명해보면 각 숫자들의 대해 더블 카운팅 형식으로 세주었다. 그걸 계산해주기 위해 prefix sum, lowerbound, upperbound 등을 계산해줬었는데 이거보다 간결한 풀이가 있을 거라고 생각한다.
#include <bits/stdc++.h>
#define fastio cin.tie(0)->ios::sync_with_stdio(0);
using namespace std;
typedef long long ll;
typedef pair<ll,ll> pii;
const ll NMAX = 5e5;
ll N, a[NMAX + 10], b[NMAX + 10];
vector<ll> indices[NMAX + 10][2], indices2[NMAX + 10][2]; //indices of species i
vector<ll> prefix[NMAX + 10], prefix2[NMAX + 10];
set<ll> species;
void solve(){
for(ll i=0;i<N;i++){
indices[a[i]][0].push_back(N-i);
indices[b[i]][1].push_back(i);
species.insert(a[i]);
}
auto it = species.begin();
while(it != species.end()){
sort(indices[*it][0].begin(),indices[*it][0].end());
prefix[*it].push_back(0);
for(ll i=0;i<indices[*it][0].size();i++){
prefix[*it].push_back(prefix[*it][i]+indices[*it][0][i]);
}
it = next(it);
}
ll ans = 0;
for(ll i=0;i<N;i++){
if(a[i] == b[i]){
ans += (i*(i+1))/2;
ans += ((N-i)*(N-i-1))/2;
}
}
it = species.begin();
while(it != species.end()){
for(ll i=0;i<indices[*it][1].size();i++){
ll ub = upper_bound(indices[*it][0].begin(),indices[*it][0].end(),
N-indices[*it][1][i]) - indices[*it][0].begin();
ub --; if(ub < 0) continue;
ll lb = upper_bound(indices[*it][0].begin(),indices[*it][0].begin()+ub+1,
indices[*it][1][i]+1) - indices[*it][0].begin(); lb--;
if(lb == -1 && indices[*it][0][0] < indices[*it][1][i]+1) lb = 0;
ans += prefix[*it][lb+1];
ans += (ub-lb)*(indices[*it][1][i]+1);
}
it = next(it);
}
species.clear();
for(ll i=0;i<N;i++){
indices2[b[i]][0].push_back(N-i);
indices2[a[i]][1].push_back(i);
species.insert(b[i]);
}
it = species.begin();
while(it != species.end()){
sort(indices2[*it][0].begin(),indices2[*it][0].end());
prefix2[*it].push_back(0);
for(ll i=0;i<indices2[*it][0].size();i++){
prefix2[*it].push_back(prefix2[*it][i]+indices2[*it][0][i]);
}
it = next(it);
}
it = species.begin();
while(it != species.end()){
for(ll i=0;i<indices2[*it][1].size();i++){
ll ub = lower_bound(indices2[*it][0].begin(),indices2[*it][0].end(),
N-indices2[*it][1][i]) - indices2[*it][0].begin();
ub --; if(ub < 0) continue;
ll lb = upper_bound(indices2[*it][0].begin(),indices2[*it][0].begin()+ub+1,
indices2[*it][1][i]+1) - indices2[*it][0].begin(); lb--;
if(lb == -1 && indices2[*it][0][0] < indices2[*it][1][i]+1) lb = 0;
ans += prefix2[*it][lb+1];
ans += (ub-lb)*(indices2[*it][1][i]+1);
}
it = next(it);
}
cout << ans;
}
int main(){
fastio;
cin >> N;
for(ll i=0;i<N;i++) cin >> a[i];
for(ll i=0;i<N;i++) cin >> b[i];
solve();
}'Computer Science' 카테고리의 다른 글
| PS Diary #7 (4) | 2025.01.23 |
|---|---|
| PS Diary #6 (0) | 2025.01.16 |
| PS Diary #5 (1) | 2025.01.15 |
| PS Diary #4 (2) | 2025.01.02 |
| PS Diary #3 (1) | 2024.12.26 |
