티스토리 뷰
이항게수와 관련된 PS를 하다가 범위가 큰 $n$과 범위가 큰 $r$에 대해서 ${n \choose r}$의 일의 자리 수를 구해야하는 일이 생겼다. 일반적인 콤비네이션 계산($O(n)$)을 하고 일의 자리수를 구하면 시간초과가 나서 다른 방법이 필요했다. 이 포스팅에서는 이와 관련된 내용을 적어보려고 한다.

1. 조합을 계산하는 일반적인 방법
가장 쉬운 방법으로는 정의식대로 $n!$, $(n-r)!$, $r!$을 모두 계산해주고 연산해주는 것이다. 하지만 $n$과 $r$이 조금만 커져도 계산 시간이 오래걸리고 PS에서는 정수형 범위나 심지어는 long long 범위까지 넘어갈 수 있기 때문에 좋지 않은 방법이다.
int factorial(int n)
{
int output = 1;
for(int i = 1; i <= n; i++)
{
output *= i;
}
return output;
}
int combination(int n, int r)
{
return factorial(n)/(factorial(r)*factorial(n-r));
}
두 번째 방법은 $n!$, $(n-r)!$, $r!$을 따로 계산하지 않고 곱셈과 나눗셈을 동시에 처리해주는 방법이다.
$$\frac{n(n-1)\cdot\cdot\cdot(n-r+1)}{r(r-1)\cdot\cdot\cdot2\cdot1}$$
int combination(int n, int r)
{
int output = 1;
for(int i=1;i<=r;i++)
{
output *= n-i+1;
output /= i;
}
return output;
}
세 번째 방법은 이항계수의 성질을 이용한 방법이다. 아래와 같은 관계식을 이용해 재귀함수로 구현할 수도 있고, 2차원 DP로 계산할 수도 있다.

int combination(int n, int r)
{
if(n==r || r==0)
{
return 1;
}
return combination(n-1,r-1)+combination(n-1,r);
}
이렇게 구한 값에 대한 $p$에 대한 나머지를 구하기만 하면 된다.
combination(n,r)%p
하지만 가장 짧은 시간이 걸리는 두 번째 방법의 시간복잡도가 $O(n)$이며, 큰 자리수 연산을 할 때 시간이 오래 걸린다. 이 보다 더 적은 시간을 요구하는 문제에서 적용하기 어렵다.
2. 루카스 정리

루카스정리는 위와 같은 공식으로 나타내진다. 이때 $m_{i}$ 는 $m$을 $p$진수로 표현했을 때 뒤에서부터 $i$번째 자리수를 의미하고 $n_{i}$도 마찬가지이다. 즉 ${m \choose n}$은 ${m_{i} \choose n+{i}}$들의 곱으로 나타낼 수 있다는 것이다.
p.f.)
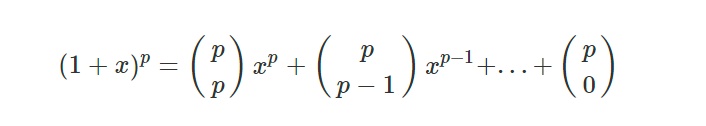
먼저 이항정리를 써보자. 그럼 $(1+x)^p$를 다음과 같이 나타낼 수 있다. 이때 이 식을 $(mod\space p)$에 대해서 보면, ${p \choose p-1}$부터 ${p \choose 1}$까지는 모두 $p$의 배수이므로 $1 + x^p$와 $(1+x)^p$는 $(mod\space p)$에 대해 합동이다. 이것을 이용해 증명을 할 것이다.
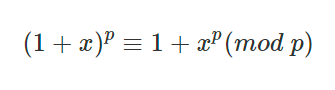
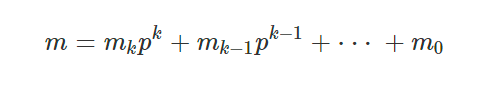
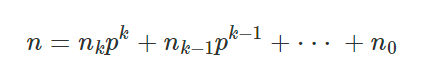
$m$과 $n$을 위와 같이 $p$진수로 표현해보면 아래와 같은 식을 얻을 수 있다.

여기서 $x^n$의 계수를 살펴보자. 오른쪽 식에서 $x^{p^i}$이 곱해진 횟수를 $n_{i}$라고 정의하자. 그러면 아래와 같이 표현된다.

$n$을 $p$진수로 표현하는 방법이 유일하기 때문에 각각의 $n_{i}$는 유일하게 결정된다. 또 여기서 계수는 아래와 같이 표현된다.

왼쪽 식에 경우는 당연히 ${m \choose n}$이므로,

다음 식이 성립하기 때문에 증명이 된다.
#include <iostream>
#include <vector>
using namespace std;
int combination(int m, int n)
{
if(m<n)
{
return 0;
}
int output = 1;
for(int i=1;i<=n;i++)
{
output *= (m-i+1);
output /= i;
}
return output;
}
vector<int> p_digit(int k, int p) {
vector<int> k_p;
while (k > 0) {
k_p.push_back(k % p);
k /= p;
}
return k_p;
}
int main()
{
int m,n,p,k1,k2,output=1;
cin>>m>>n>>p;
k1 = p_digit(n,p).size();
k2 = p_digit(m,p).size();
for(int i=0;i<k2;i++)
{
output *= combination(p_digit(m,p)[i],p_digit(n,p)[i]);
}
cout<<output%p;
}
루카스정리를 이용해 $m$,$n$,$p$가 주어진 경우 ${m \choose n}$을 $p$로 나눈 나머지를 구할 수 있다. $10$으로 나눈 나머지를 구하려면 $2$와 $5$에 대해 구하고 연립해주면 된다.
'Mathmatics' 카테고리의 다른 글
| 수리 창의문제해결 프로젝트 1차 (1) | 2024.10.26 |
|---|---|
| 피보나치 수열의 성질 (1) | 2024.07.29 |
| FTC$($Fundamental Theorem of Calculus$)$ 증명 (0) | 2024.07.25 |
| 격자 도형의 넓이 구하는 픽의 정리(Pick's theorem) (1) | 2024.01.03 |
| 몬즈의 정리(Monge's Theorem) (0) | 2023.12.23 |
